题目内容
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间![]() 的最小值.
的最小值.
【答案】见解析
【解析】(1)由![]() ω+φ=0,
ω+φ=0,![]() ω+φ=π可得ω=
ω+φ=π可得ω=![]() ,φ=-
,φ=-![]() ,
,
由![]() x1-
x1-![]() =
=![]() ,
,![]() x2-
x2-![]() =
=![]() ,
,![]() x3-
x3-![]() =2π可得x1=
=2π可得x1=![]() ,x2=
,x2=![]() ,x3=
,x3=![]() ,
,
又Asin![]() =2,∴A=2,
=2,∴A=2,
∴f(x)=2sin![]() .
.
(2)函数f(x)=2sin![]() 的图象向左平移π个单位,得g(x)=2sin
的图象向左平移π个单位,得g(x)=2sin![]() =2cos
=2cos![]() 的图象,
的图象,
∴y=f(x)g(x)=2sin![]() ·2cos
·2cos![]() =2sin
=2sin![]() .
.
∵x∈![]() ,∴x-
,∴x-![]() ∈
∈![]() ,
,
∴当x-![]() =-
=-![]() ,即x=
,即x=![]() 时,y=f(x)·g(x)取得最小值-2.
时,y=f(x)·g(x)取得最小值-2.

【题目】据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
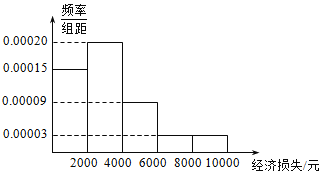
(1)若先从损失超过6000元的居民中随机抽出2户进行调查,求这2户不在同一小组的概率;(2)洪灾过后小区居委会号召小区居民为洪灾重灾区捐款,小王调查的50户居民的捐款情况如表,在表格空白处填写正确的数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?

P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:K2=![]() .
.