题目内容
【题目】点O是平面上一定点,A、B、C是平面上△ABC的三个顶点,∠B、∠C分别是边AC、AB的对角,以下命题正确的是(把你认为正确的序号全部写上). ①动点P满足 ![]() =
= ![]() +
+ ![]() +
+ ![]() ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;
②动点P满足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),则△ABC的内心一定在满足条件的P点集合中;
)(λ>0),则△ABC的内心一定在满足条件的P点集合中;
③动点P满足 ![]() =
= ![]() +λ(
+λ( 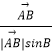 +
+ 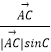 )(λ>0),则△ABC的重心一定在满足条件的P点集合中;
)(λ>0),则△ABC的重心一定在满足条件的P点集合中;
④动点P满足 ![]() =
= ![]() +λ(
+λ( 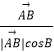 +
+ 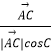 )(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
)(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
⑤动点P满足 ![]() =
= ![]() +λ(
+λ( 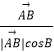 +
+ 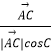 )(λ>0),则△ABC的外心一定在满足条件的P点集合中.
)(λ>0),则△ABC的外心一定在满足条件的P点集合中.
【答案】①②③④⑤
【解析】解:对于①,∵动点P满足 ![]() =
= ![]() +
+ ![]() +
+ ![]() , ∴
, ∴ ![]() =
= ![]() +
+ ![]() ,
,
则点P是△ABC的重心,故①正确;
对于②,∵动点P满足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
又 ![]() +
+ ![]() 在∠BAC的平分线上,
在∠BAC的平分线上,
∴ ![]() 与∠BAC的平分线所在向量共线,
与∠BAC的平分线所在向量共线,
∴△ABC的内心在满足条件的P点集合中,②正确;
对于③,动点P满足 ![]() =
= ![]() +λ(
+λ( 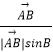 +
+ 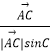 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 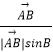 +
+ 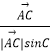 ),(λ>0),
),(λ>0),
过点A作AD⊥BC,垂足为D,则| ![]() |sinB=|
|sinB=| ![]() |sinC=AD,
|sinC=AD,![]() =
= ![]() (
( ![]() +
+ ![]() ),向量
),向量 ![]() +
+ ![]() 与BC边的中线共线,
与BC边的中线共线,
因此△ABC的重心一定在满足条件的P点集合中,③正确;
对于④,动点P满足 ![]() =
= ![]() +λ(
+λ( 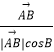 +
+ 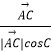 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 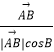 +
+ 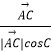 )(λ>0),
)(λ>0),
∴ ![]()
![]() =λ(
=λ( 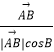 +
+ 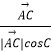 )
) ![]() =λ(|
=λ(| ![]() |﹣|
|﹣| ![]() |)=0,
|)=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴△ABC的垂心一定在满足条件的P点集合中,④正确;
对于⑤,动点P满足 ![]() =
= ![]() +λ(
+λ( 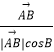 +
+ 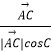 )(λ>0),
)(λ>0),
设 ![]() =
= ![]() ,
,
则 ![]() =λ(
=λ( 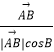 +
+ 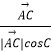 ),
),
由④知( 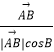 +
+ 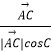 )
) ![]() =0,
=0,
∴ ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴P点的轨迹为过E的BC的垂线,即BC的中垂线;
∴△ABC的外心一定在满足条件的P点集合,⑤正确.
故正确的命题是①②③④⑤.
所以答案是:①②③④⑤.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.