题目内容
19.点S在平面ABC外,SB⊥AC,SB=AC=4,E、F分别是SC和AB的中点,则EF的长是( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
分析 先取BC的中点D,连接ED与FD,根据中位线定理可知ED∥SB,FD∥AC,根据题意可知三角形EDF为等腰直角三角形,然后解三角形即可.
解答 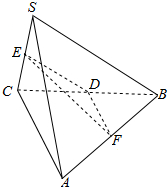 解:取BC的中点D,连接ED与FD,
解:取BC的中点D,连接ED与FD,
∵E、F分别是SC和AB的中点,点D为BC的中点,
∴ED∥SB,FD∥AC,
而SB⊥AC,SB=AC=4,则三角形EDF为等腰直角三角形,
则ED=FD=2,即EF=$2\sqrt{2}$.
故选:A.
点评 本题主要考查了中位线定理,以及异面直线所成角的应用,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
相关题目
10.正四棱锥P-ABCD的高为$\sqrt{3}$,侧棱长为$\sqrt{7}$,则它的斜高为( )
| A. | 2 | B. | 4 | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
9.已知圆C1:x2+y2-4x-4y-1=0,圆C2:x2+y2+2x+8y-8=0,圆C1与圆C2的位置关系为( )
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |
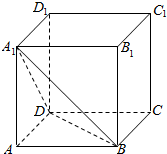 如图,在棱长为a的正方体ABCD-A1B1C1D1中,求A到平面A1BD的距离d.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,求A到平面A1BD的距离d.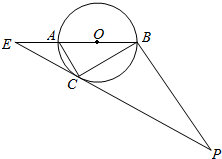 如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
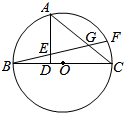 如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,做AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.
如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,做AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.