题目内容
4.下列说法中:①两条直线都和同一个平面平行,则这两条直线平行;
②在平行投影下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小完全相同;
③一个圆绕其任意一条直径旋转180°所形成的旋转体叫做球;
④a∥b,b?α⇒a∥α;
⑤已知三条两两异面的直线,则存在无穷多条直线与它们都相交.
则正确的序号是②⑤.
分析 由和同一个平面平行的两直线的位置关系判断①;由平行投影的特点判断②;由球的概念判断③;由a∥b,b?α⇒a∥α或a?α判断④;画出图形说明⑤正确.
解答  解:对于①,两条直线都和同一个平面平行,则这两条直线的关系是平行、相交或异面,①错误;
解:对于①,两条直线都和同一个平面平行,则这两条直线的关系是平行、相交或异面,①错误;
对于②,在平行投影下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小完全相同,②正确;
对于③,根据球的定义可知,以圆的直径所在直线为旋转轴,圆面旋转一周形成的旋转体叫做球,③错误;
对于④,a∥b,b?α⇒a∥α或a?α,④错误;
对于⑤,构造长方体ABCD-A′B′C′D′,取直线AB为a,DD′为b,C′E为c,其中E为BC的中点,则a、b、c两两异面,
由于直线DE与AB相交,故DE与三异面直线同时相交.
过AB作平面交DD′、CC′、EC′分别于F、G、H,当G与C′不重合时,直线FH必与AB相交,即FH与三异面直线同时相交,又过AB作满足条件的平面有无数个,
故与三异面直线同时相交的直线有无数条,⑤正确.
故答案为:②⑤.
点评 本题考查命题的真假判断与应用,考查了空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
19.点S在平面ABC外,SB⊥AC,SB=AC=4,E、F分别是SC和AB的中点,则EF的长是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
9.已知$f(x)=\left\{\begin{array}{l}{|lg|x||\\;x≠0}\\{0\\;x=0}\end{array}\right.$,关于x的方程f2(x)+bf(x)+c=0有7个不同的解,则满足b,c的条件是( )
| A. | b<0,c<0 | B. | b<0,c=0 | C. | b>0,c=0 | D. | b>0,c<0 |
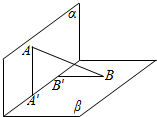 如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )