题目内容
9.设点F是△ABC的边AB上的中点,O为任意点,求证:$\overrightarrow{OF}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$.分析 根据向量加法的平行四边法则,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OE}$,而$\overrightarrow{OE}$=2$\overrightarrow{OF}$,可以推出$\overrightarrow{OF}$=$\frac{1}{2}$$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$).
解答 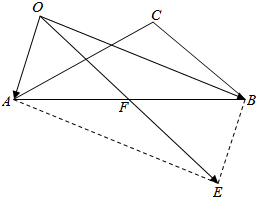 证明:如右图,O为任意一点,F为AB的中点,
证明:如右图,O为任意一点,F为AB的中点,
以OA,OB为邻边构造平行四边形OAEB,
其对角线AB,OE互相平分,
即F为AB的中点,也是OE的中点,
根据向量加法的平行四边法则,
$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OE}$,
而$\overrightarrow{OE}$=2$\overrightarrow{OF}$,
所以,$\overrightarrow{OF}$=$\frac{1}{2}$$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$),即证.
点评 本题主要考查了向量加法的几何意义,涉及平行四边形法则和平行四边形的性质,属于基础题.

练习册系列答案
相关题目
18.小明利用课余时间收集废品,将卖得的28元钱购买5本大小不同的笔记本,两种笔记本的页数和价格如表:
小明计划买到的笔记本总页数不低于340页,他应当怎样购买才能花钱最少?
| 大笔记本 | 小笔记本 | |
| 价格(元/本) | 6 | 5 |
| 页数(页/本) | 100 | 60 |
1.三棱锥P-ABC三条侧棱两两垂直,PA=a,PB=b,PC=c,三角形ABC的面积为S,则顶点P到底面的距离是( )
| A. | $\frac{abc}{6s}$ | B. | $\frac{abc}{3s}$ | C. | $\frac{abc}{2s}$ | D. | $\frac{abc}{s}$ |
19.点S在平面ABC外,SB⊥AC,SB=AC=4,E、F分别是SC和AB的中点,则EF的长是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |