题目内容
11.在四面体A-BCD中,E,F分别是AB,CD的中点,若AC,BD所成的角为60°,且BD=AC=1,求EF的长度.
分析 先确定BD、AC所成的角,再在三角形中,利用余弦定理,可求EF的长.
解答 解:取BC的中点G,连接EG、FG,则∠EGF(或其补角)为BD、AC所成的角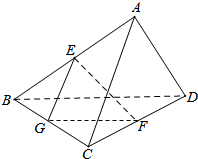
∵BD、AC所成的角为60°,∴∠EGF=60°或120°
∵BD=AC=1,∴EG=FG=$\frac{1}{2}$
∴∠EGF=60°时,EF=$\frac{1}{2}$;∠EGF=120°时,EF=$\sqrt{\frac{1}{4}+\frac{1}{4}-2×\frac{1}{2}×\frac{1}{2}×cos120°}$=$\frac{\sqrt{3}}{2}$,
∴EF=$\frac{1}{2}$或$\frac{\sqrt{3}}{2}$
故答案为:$\frac{1}{2}$或$\frac{\sqrt{3}}{2}$.
点评 本题考查空间角,考查学生的计算能力,正确确定BD、AC所成的角是关键.

练习册系列答案
相关题目
1.三棱锥P-ABC三条侧棱两两垂直,PA=a,PB=b,PC=c,三角形ABC的面积为S,则顶点P到底面的距离是( )
| A. | $\frac{abc}{6s}$ | B. | $\frac{abc}{3s}$ | C. | $\frac{abc}{2s}$ | D. | $\frac{abc}{s}$ |
19.点S在平面ABC外,SB⊥AC,SB=AC=4,E、F分别是SC和AB的中点,则EF的长是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
3.若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
20.平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°,$\overrightarrow a$=(2,0),|$\overrightarrow b$|=1,则|$\overrightarrow a$+2$\overrightarrow b$|=( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 12 | D. | $\sqrt{10}$ |
 如图所示,正三棱柱ABC-A1B1C1的底面边长与侧棱长均为2,D为AC中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长与侧棱长均为2,D为AC中点.