题目内容
20．将数列{an}中的所有项按每一行比上一行多两项的规则排成如下数表：a1
a2 a3 a4
a5 a6 a7 a8 a9
…
已知表中的第一列数a1，a2，a5，…构成一个等差数列，且知a2=4，a10=10．从第二行起，即每一行中的数按从左到右的顺序均构成以$\frac{1}{2}$为公比的等比数列，则a100=$\frac{7}{{2}^{17}}$．
分析 确定a100为第10行的最后一个数，第10行的第一个数为28，共19个数，即可得出结论．
解答 解：∵第一列数a1，a2，a5，…构成一个等差数列，且知a2=4，a10=10，
∴第一列数组成以1为首项，3为公差的等差数列．
又前n行共有n2项，∴a100为第10行的最后一个数，
∵第10行的第一个数为28，∴a100=28$•（\frac{1}{2}）^{19}$=$\frac{7}{{2}^{17}}$．
故答案为：$\frac{7}{{2}^{17}}$．
点评 本题考查数列的性质和应用，本题解题的关键是a100为第10行的最后一个数，第10行的第一个数为28，共19个数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，它是一个算法的流程图，最后输出的k值为5．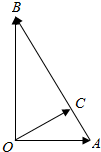
如图所示，已知∠B=30°，∠A0B=90°，点C在AB上，0C⊥AB，用$\overrightarrow{OA}和\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$，则$\overrightarrow{OC}$等于$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$．
15．设m、n是不同的直线，α、β是不同的平面，有以下四个命题：
①若m⊥n，m⊥α，则n∥α
②若n⊥β，m∥α，α⊥β，则m∥n
③若m⊥α，m∥β，则α⊥β
④若m∥n，n?α，则m∥α
其中真命题的个数是（ ）
①若m⊥n，m⊥α，则n∥α
②若n⊥β，m∥α，α⊥β，则m∥n
③若m⊥α，m∥β，则α⊥β
④若m∥n，n?α，则m∥α
其中真命题的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |