题目内容
10. 已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.
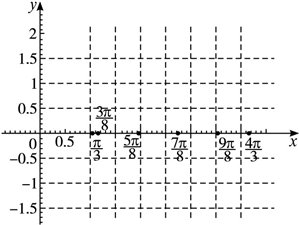
已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.(1)在所给坐标系中用五点法作出它在区间[$\frac{π}{8}$,$\frac{9π}{8}$]上的图象.
(2)求f(x)的单调区间.
(3)说明f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的图象可由y=sinx的图象经过怎样的变换而得到.
分析 (1)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
(2)由复合函数的单调性的求法求解函数的单调增区间;
(3)根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 (本题满分为12分)
解:(1)列表:
| 2x+$\frac{π}{4}$ | π | $\frac{3}{2}$π | 2π | $\frac{5}{2}$π |
| x | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$) | 0 | -$\sqrt{2}$ | 0 | $\sqrt{2}$ |
 …4分
…4分(2)由-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,得f(x)的单调增区间为:$[{-\frac{3π}{8}+kπ,\frac{π}{8}+kπ}],k∈Z$.
由$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{3π}{2}$+2kπ,得f(x)的单调减区间为:$[{\frac{π}{8}+kπ,\frac{5π}{8}+kπ}],k∈Z$…8分
(3)把y=sinx的图象向左平移$\frac{π}{4}$个单位,得到y=sin(x+$\frac{π}{4}$)的图象,再把所得图象上点的
纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$,得到y=sin(2x+$\frac{π}{4}$)的图象,最后把所得图象上点的横坐标不变,
纵坐标扩大到原来的$\sqrt{2}$倍得到y=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的图象;…12分
点评 本题主要考查用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.41(6)对应的二进制数是( )
| A. | 11001(2) | B. | 10011(2) | C. | 10101(2) | D. | 10001(2) |