题目内容
4.在△ABC中,A=60°,B=75°,c=3,求C,a,b.分析 由三角形内角和可得C,再由正弦定理可得a和b值.
解答 解:∵在△ABC中,A=60°,B=75°,c=3,
∴C=180°-(60°+75°)=45°,
∴由正弦定理可得a=$\frac{csinA}{sinC}$=$\frac{3×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=$\frac{3\sqrt{6}}{2}$,
b=$\frac{csinB}{sinC}$=$\frac{3×(\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2})}{\frac{\sqrt{2}}{2}}$=$\frac{3\sqrt{3}+3}{2}$.
点评 本题考查解三角形,涉及正弦定理的应用和两角和与差的三角函数公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知直线l的方程为y=$\sqrt{3}$x+1,则该直线l的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
15.lg2+lg5=( )
| A. | lg7 | B. | lg25 | C. | 1 | D. | lg32 |
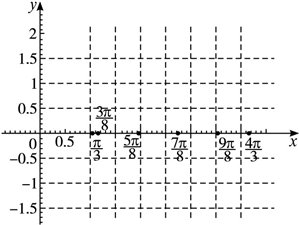 已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.
已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.