题目内容
5.判断方程x2-cosx=0的根的个数.分析 分别作出函数y=x2和y=cosx的图象,利用函数图象的交点判断方程根的个数.
解答 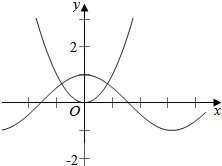 解:方程x2-cosx=0的根的个数,即为
解:方程x2-cosx=0的根的个数,即为
函数y=x2和y=cosx的交点个数,
分别作出函数y=x2和y=cosx的图象,
由图象可知两个图象的交点个数为2个,
即方程x2-cosx=0的实根个数为2个.
点评 本题主要考查方程个数的判断,将方程转化为函数,利用函数图象的交点个数,即可判断方程根的个数,利用数形结合是解决此类问题的基本方法.

练习册系列答案
相关题目
15.lg2+lg5=( )
| A. | lg7 | B. | lg25 | C. | 1 | D. | lg32 |
11.若命题p:?x0∈R,使x02+(a-1)x0+1<0,则该命题的否定¬p为( )
| A. | ?x0∉R,使x02+(a-1)x0+1<0 | B. | ?x∈R,x2+(a-1)x+1<0 | ||
| C. | ?x0∈R,使x02+(a-1)x0+1≥0 | D. | ?x∈R,x2+(a-1)x+1≥0 |
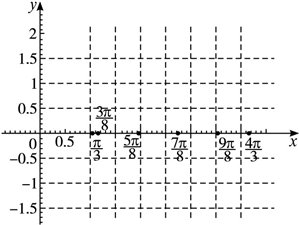 已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.
已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),x∈R.