题目内容
已知双曲线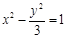 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则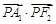 的最小值为( )
的最小值为( )
| A.-2 | B. | C.1 | D.0 |
A
解析试题分析:由双曲线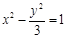 ,得左顶点
,得左顶点 ,右焦点
,右焦点 ,设右支上一点
,设右支上一点 ,则
,则 ,∴
,∴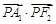 =
= ,又∵
,又∵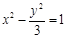 ,∴
,∴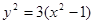 ,代入上式,可得
,代入上式,可得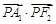 =
= ,当
,当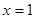 时,
时,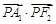 最小值为-2,选A.
最小值为-2,选A.
考点:1、向量的数量积运算;2、函数的最小值;3、双曲线的标准方程.

练习册系列答案
相关题目
已知抛物线的顶点在原点,焦点在 轴上,抛物线上的点到焦点的距离为4,则的值为( )
轴上,抛物线上的点到焦点的距离为4,则的值为( )
| A.4 | B.-2 | C.4或-4 | D.12或-2 |
与圆 及圆
及圆 都相外切的圆的圆心在( )
都相外切的圆的圆心在( )
| A.一个椭圆上 | B.一支双曲线上 | C.一条抛物线上 | D.一个圆上 |
与椭圆 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )
A. | B. | C. | D. |
已知直线 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线 和直线
和直线 的距离之和的最小值是( )
的距离之和的最小值是( )
A. | B.2 | C. | D.3 |
设双曲线 的半焦距为
的半焦距为 ,直线
,直线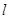 过
过 两点,若原点
两点,若原点 到
到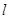 的距离为
的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. 或2 或2 | B.2 | C. 或 或 | D. |
若双曲线 的渐近线与圆
的渐近线与圆 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )
A. | B. | C.2 | D. |
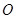 为坐标原点,
为坐标原点, 为抛物线
为抛物线 的焦点,
的焦点, 为
为 上一点,若
上一点,若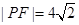 ,则
,则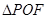 的面积为( )
的面积为( )
A. | B. | C. | D. |



