题目内容
已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于点A,B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
A. | B. | C. | D. |
B
解析试题分析:设抛物线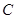 :
: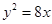 的准线为
的准线为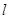 :
: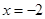 ,直线
,直线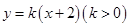 横过定点
横过定点 ,如图所示,
,如图所示,
过点 ,
, 分别作
分别作 于点
于点 ,
,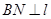 于点
于点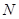 ,则由抛物线的定义可知,
,则由抛物线的定义可知,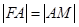 ,
,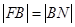 ,又因为
,又因为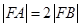 ,所以
,所以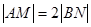 ,由
,由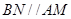 得
得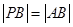 ,则点
,则点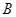 是线段
是线段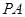 的中点,连接
的中点,连接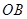 ,则
,则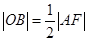 ,所以
,所以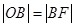 ,那么
,那么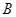 点横坐标为1,将
点横坐标为1,将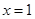 代入抛物线方程,解得
代入抛物线方程,解得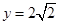 ,所以有
,所以有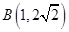 ,代入直线方程解得
,代入直线方程解得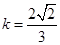 .
.
考点:1、抛物线的定义及性质的应用;2、平行线分线段成比例定理.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
过双曲线 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则 (F2为右焦点)的周长是( )
(F2为右焦点)的周长是( )
| A.28 | B.22 | C.14 | D.12 |
已知斜率为2的直线 双曲线
双曲线 交
交 两点,若点
两点,若点 是
是 的中点,则
的中点,则 的离心率等于( )
的离心率等于( )
A. | B.2 | C. | D. |
已知双曲线 的中心在原点,焦点在坐标轴上,
的中心在原点,焦点在坐标轴上, 是
是 上的点,且
上的点,且 是
是 的一条渐近线,则
的一条渐近线,则 的方程为( )
的方程为( )
A. | B. |
C. 或 或 | D. 或 或 |
双曲线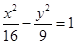 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C. | D.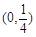 |
已知双曲线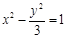 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则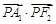 的最小值为( )
的最小值为( )
| A.-2 | B. | C.1 | D.0 |
抛物线y2= 2x的准线方程是( )
A.y= | B.y=- | C.x= | D.x=-  |
 的一个焦点
的一个焦点 作一条渐近线的垂线,垂足为点
作一条渐近线的垂线,垂足为点 ,与另一条渐近线交于点
,与另一条渐近线交于点 ,若
,若 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )

