题目内容
与椭圆 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )
A. | B. | C. | D. |
B
解析试题分析:在椭圆 中,
中, ,∴
,∴ ,∴焦点为
,∴焦点为 ,设所求的双曲线方程为:
,设所求的双曲线方程为:
 ,由双曲线的定义可知:
,由双曲线的定义可知: ,∴
,∴ ,∴
,∴ ,故双曲线方程为:
,故双曲线方程为: .
.
考点:椭圆和双曲线的定义及标准方程.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
双曲线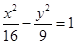 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
已知直线 和直线
和直线 ,抛物线
,抛物线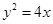 上一动点P到直线
上一动点P到直线 和直线
和直线 的距离之和的最小值是( )
的距离之和的最小值是( )
A. | B.2 | C. | D.3 |
已知双曲线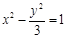 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则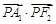 的最小值为( )
的最小值为( )
| A.-2 | B. | C.1 | D.0 |
若 是2和8的等比中项,则圆锥曲线
是2和8的等比中项,则圆锥曲线 的离心率是( )
的离心率是( )
A. | B. | C. 或 或 | D. |
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )







 的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2
的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2 ,则△
,则△ 的周长是( )
的周长是( )


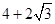
 是双曲线
是双曲线 上的不同三点,且
上的不同三点,且 连线经过坐标原点,若直线
连线经过坐标原点,若直线 的斜率乘积
的斜率乘积 ,则该双曲线的离心率
,则该双曲线的离心率 =( )
=( )