题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且方程
,且方程![]() 有一根为
有一根为![]()
(1)求![]() 、
、![]() ;
;
(2)求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)分别取![]() ,根据方程
,根据方程![]() 有一根
有一根![]() ,,即可求得
,,即可求得![]() 、
、![]() ;(2)由题设得
;(2)由题设得![]() ,,即即
,,即即![]() 当
当![]() 时,
时,![]() ,代入上式得
,代入上式得![]() ,通过计算猜想
,通过计算猜想![]() 再用数学归纳法证明这个结论,进而利用当
再用数学归纳法证明这个结论,进而利用当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,适合上式,即可求得
,适合上式,即可求得![]() 的通项公式.
的通项公式.
试题解析:(1)![]() 时,
时,![]() 有一根
有一根![]() ,
,
于是![]() ,解得
,解得![]() .
.
![]() 时,
时,![]() 有一根
有一根![]() ,
,
于是![]() ,解得
,解得![]() .
.
(2)由题设,得![]() ,
,
即![]() ①
①
当![]() 时,
时,![]() ,代入①得
,代入①得![]() .②
.②
由于(1)知![]() .
.
由②可![]() ,由此猜想
,由此猜想![]() ,
,
下面用数学归纳法证明这个结论.
(ⅰ)![]() 时,已知结论成立.
时,已知结论成立.
(ⅱ)假设![]() 时结论成立,即
时结论成立,即![]() ,当
,当![]() 时,由②得
时,由②得![]() ,
,
即![]() ,故
,故![]() 时结论也成立.
时结论也成立.
综上,由(ⅰ)、(ⅱ)可知,![]() 对所有正整数
对所有正整数![]() 都成立,于是当
都成立,于是当![]() 时,
时,![]() ,
,
又因为![]() 时,
时,![]() ,所以
,所以![]() 的通项公式为
的通项公式为![]() .
.

【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: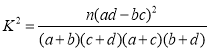
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
参考公式与临界值表: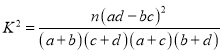 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |


