题目内容
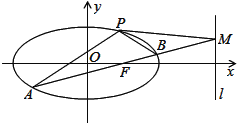
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数![]() 模型.园区服务中心P在x轴正半轴上,PO=
模型.园区服务中心P在x轴正半轴上,PO=![]() 百米.
百米.

(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道直线段PQ最短.
【答案】(1) ![]() 的最小值为
的最小值为![]() 百米.
百米.
(2) 当点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米,通道PQ最短.
百米,通道PQ最短.
【解析】
(1)设![]() ,
,![]() ,求出
,求出![]()
![]() ,再利用基本不等式求OM的最短长度.(2) 当直线
,再利用基本不等式求OM的最短长度.(2) 当直线![]() 与边界曲线相切时,
与边界曲线相切时,![]() 最短.设切点为
最短.设切点为![]() ,求出切点为
,求出切点为![]() ,切线方程为
,切线方程为![]() ,令
,令![]() ,得
,得![]() ,即点
,即点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米.
百米.
(1)设![]() ,
,![]() ,
,
则![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
所以![]() 的最小值为
的最小值为![]() 百米.
百米.
(2)当直线![]() 与边界曲线相切时,
与边界曲线相切时,![]() 最短.
最短.
设切点为![]() ,由
,由![]() 得
得![]() ,
,
所以切线的方程为![]() .
.
因为![]() 在
在![]() 轴正半轴上,且PO=
轴正半轴上,且PO=![]() ,所以
,所以![]() 点坐标为
点坐标为![]() .
.
因为切线过点![]() ,所以
,所以![]() ,
,
整理得![]() ,解得
,解得![]() ,或
,或![]() .
.
因为![]() ,所以
,所以![]() ,此时切点为
,此时切点为![]() ,切线方程为
,切线方程为![]() .
.
令![]() ,得
,得![]() ,即点
,即点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米.
百米.
答:当点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米,通道PQ最短.
百米,通道PQ最短.

练习册系列答案
相关题目