题目内容
【题目】已知双曲线方程为![]() .
.
(1)已知直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中点在圆
的中点在圆![]() 上,求
上,求![]() 的值;
的值;
(2)设直线![]() 是圆
是圆![]() 上动点
上动点![]() 处的切线,
处的切线,![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,证明
,证明![]() 的大小为定值.
的大小为定值.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)将直线方程与双曲线方程联立,利用一元二次方程根与系数的关系、中点坐标公式,结合题意进行求解即可;
(2)先求出直线![]() 的方程,与双曲线联立,利用一元二次方程根与系数关系,结合平面向量夹角公式进行证明即可.
的方程,与双曲线联立,利用一元二次方程根与系数关系,结合平面向量夹角公式进行证明即可.
(1)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,由
,由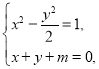 得
得![]() ,
,![]() ,
,
![]() .
.
点![]() 在圆
在圆![]() 上,
上,![]()
(2)点![]() 在圆
在圆![]() 上,所以有
上,所以有![]() ,
,
因为![]() ,所以设过
,所以设过![]() 与该圆相切的直线的斜率为
与该圆相切的直线的斜率为![]() ,
,
因此有![]() ,所以切线方程为:
,所以切线方程为:![]() ,
,
化简,得![]() .由
.由 及
及![]() ,得
,得![]() .∵切线
.∵切线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,且
,且![]() .设
.设![]() 两点的坐标分别为
两点的坐标分别为![]() ,则
,则![]() .
.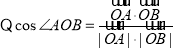 ,且
,且![]()
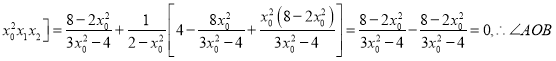 的大小为90°.
的大小为90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某电器商场销售的彩电、U盘和![]() 播放器三种产品.该商场的供货渠道主要是甲、乙两个品牌的二级代理商.今年9月份,该商场从每个代理商处各购得彩电100台、U盘52个、
播放器三种产品.该商场的供货渠道主要是甲、乙两个品牌的二级代理商.今年9月份,该商场从每个代理商处各购得彩电100台、U盘52个、![]() 播放器180台.而10月份,该商场从每个代理商处购得的产品数量都是9月份的1.5倍.现知甲、乙两个代理商给出的产品单价(元)如下页表中所示:
播放器180台.而10月份,该商场从每个代理商处购得的产品数量都是9月份的1.5倍.现知甲、乙两个代理商给出的产品单价(元)如下页表中所示:
彩电 | U盘 |
| |
甲代理商单价(元) | 2350 | 1200 | 750 |
乙代理商单价(元) | 2100 | 920 | 700 |
(1)计算![]() ,并指出结果的实际意义;
,并指出结果的实际意义;
(2)用矩阵求该商场在这两个月中分别支付给两个代理商的购货费用.