题目内容
【题目】设椭圆中心在坐标原点,![]() 是它的两个顶点,直线
是它的两个顶点,直线![]() 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)解:依题设得椭圆的方程为![]() ,
,
直线![]() 的方程分别为
的方程分别为![]() ,
,![]() .············ 2分
.············ 2分
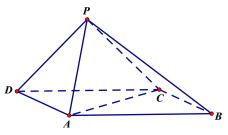
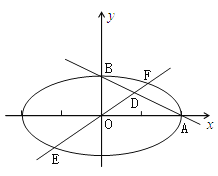
如图,设![]() ,其中
,其中![]() ,
,

且![]() 满足方程
满足方程![]() ,故
,故![]() .①
.①
由![]() 知
知![]() ,得
,得![]() ;
;
由![]() 在
在![]() 上知
上知![]() ,得
,得![]() .所以
.所以![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() .················ 6分
.················ 6分
(Ⅱ)根据点到直线的距离公式和①式知,点![]() 到
到![]() 的距离分别为
的距离分别为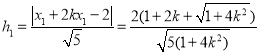 ,
,
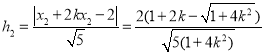 .9分
.9分
又![]() ,所以四边形
,所以四边形![]() 的面积为
的面积为
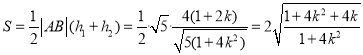
![]() ,
,
当![]() ,即当
,即当![]() 时,上式取等号.所以
时,上式取等号.所以![]() 的最大值为
的最大值为![]() .
.
【解析】
试题(Ⅰ)由题意易得椭圆方程,直线![]() 的方程,再设
的方程,再设![]() ,
,![]() 满足方程
满足方程![]() ,把
,把![]() 用坐标表示出来得
用坐标表示出来得![]() ,又点
,又点![]() 在直线
在直线![]() 上,则
上,则![]() ,根据以上关系式可解得
,根据以上关系式可解得![]() 的值;(Ⅱ)先求点E、F到AB的距离,再求
的值;(Ⅱ)先求点E、F到AB的距离,再求![]() ,则可得面积
,则可得面积![]() ,然后利用不等式求面积的最大值.
,然后利用不等式求面积的最大值.
试题解析:(I)依题意,得椭圆的方程为![]() , 1分
, 1分
直线![]() 的方程分别为
的方程分别为![]() , 2分
, 2分
如图设![]() ,其中
,其中![]() ,
,
![]() 满足方程
满足方程![]() 且故
且故![]() ,
,
由![]() 知
知![]() ,得
,得![]() , 4分
, 4分
由点![]() 在直线
在直线![]() 上知,
上知,![]() 得
得![]() , 5分
, 5分
![]() ,化简得
,化简得![]() 解得
解得![]() 或
或![]() . 7分
. 7分
(II)根据点到直线的距离公式和①式知,点E、F到AB的距离分别为
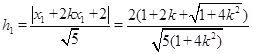 , 8分
, 8分
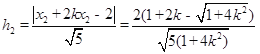 , 9分
, 9分
又![]() ,所以四边形AEBF的面积为
,所以四边形AEBF的面积为
![]()
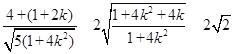 , 11分
, 11分
当![]() 即当
即当![]() 时,上式取等号,所以S的最大值为
时,上式取等号,所以S的最大值为![]() 13分
13分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目