Question

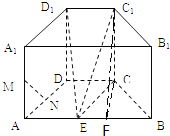
【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，M、N分别是棱AA1、AD的中点，设E是棱AB的中点．

（1）求证：MN∥平面CEC1；
（2）求平面D1EC1与平面ABCD所成角的正切值．

Answer 1

【答案】
（1）证明：∵在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为等腰梯形，

AB∥CD，AB=4，BC=CD=2，AA1=2，

M、N分别是棱AA1、AD的中点，设E是棱AB的中点，

∴DD1∥CC1，AD∥CE，

∵AD∩DD1=D，CC1∩CE=C，

AD，DD1平面A1DD1A，CC1，CE平面CEC1，

∴平面A1DD1A∥平面CEC1，

∵MN平面A1DD1A，∴MN∥平面CEC1

（2）解：平面D1EC1与平面ABCD所成角就是平面ABC1D1与平面ABCD所成的角，

∵CC1⊥平面ABCD，过C作CF⊥AB，交AB于F，连结C1F，

则∠CFC1是平面D1EC1与平面ABCD所成角，

∵CC1=AA1=2，CE=BC=BE=2，CF= = ，

∴tan∠CFC1= = = ．

∴平面D1EC1与平面ABCD所成角的正切值为

【解析】（1）推导出DD1∥CC1 ， AD∥CE，从而平面A1DD1A∥平面CEC1 ， 由此能证明MN∥平面CEC1 ． （2）平面D1EC1与平面ABCD所成角就是平面ABC1D1与平面ABCD所成的角，过C作CF⊥AB，交AB于F，连结C1F，则∠CFC1是平面D1EC1与平面ABCD所成角，由此能求出平面D1EC1与平面ABCD所成角的正切值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．