题目内容
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数).
为参数).
(1)将两曲线化成普通坐标方程;
(2)求两曲线的公共弦长及公共弦所在的直线方程.
【答案】(1)曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() ;(2)
;(2) ![]() ,
, ![]() .
.
【解析】试题分析:(1)因为![]() ,所以曲线
,所以曲线![]() 的极坐标方程
的极坐标方程![]() 化成普通坐标方程是
化成普通坐标方程是![]() ,由
,由![]() 变形得
变形得![]() ,两式平方相加可得
,两式平方相加可得![]() ,这就是曲线
,这就是曲线![]() 的普通坐标方程;(2)两圆的方程相减,可得两圆公共弦所在的直线方程,求其中一个圆的圆心到公共弦所在直线的距离,也就是弦心距,利用弦心距、弦长一半、半径的勾股数关系求弦长一半,再求弦长。
的普通坐标方程;(2)两圆的方程相减,可得两圆公共弦所在的直线方程,求其中一个圆的圆心到公共弦所在直线的距离,也就是弦心距,利用弦心距、弦长一半、半径的勾股数关系求弦长一半,再求弦长。
试题解析:解:(1)由题知,曲线![]() :
: ![]() 的直角坐标方程为:
的直角坐标方程为: ![]() ①,
①,
圆心为![]() ,半径为1;
,半径为1;
曲线![]() :
: ![]() (
(![]() 为参数)的直角坐标方程为
为参数)的直角坐标方程为![]() ②,
②,
(2)由①-②得, ![]() ,此即为过两圆的交点的弦所在的直线方程.
,此即为过两圆的交点的弦所在的直线方程.
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
故两曲线的公共弦长为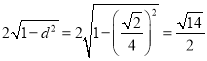 .
.

练习册系列答案
相关题目
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.

