题目内容
【题目】已知椭圆![]() :
:![]() ,过椭圆右焦点的最短弦长是
,过椭圆右焦点的最短弦长是![]() ,且点
,且点 在椭圆上.
在椭圆上.
(1)求该椭圆的标准方程;
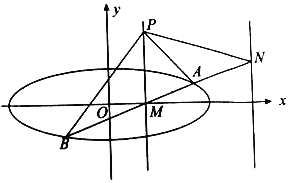
(2)设动点![]() 满足:
满足:![]() ,其中
,其中![]() ,
,![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,求点
,求点![]() 的轨迹方程并判断是否存在两个定点
的轨迹方程并判断是否存在两个定点![]() 、
、![]() ,使得
,使得![]() 为定值?若存在,求出定值;若不存在,说明理由.
为定值?若存在,求出定值;若不存在,说明理由.
【答案】(1)![]() (2)答案见解析
(2)答案见解析
【解析】
(1)因为椭圆![]() :
:![]() ,过椭圆右焦点的最短弦长是
,过椭圆右焦点的最短弦长是![]() ,可得
,可得![]() .点
.点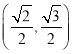 在椭圆上,可得
在椭圆上,可得![]() ,即可求得答案;
,即可求得答案;
(2)设![]() ,
,![]() ,
,![]() ,则由
,则由![]() 得:
得:![]() ,即
,即![]() ,
,![]() .点
.点![]() ,
,![]() 在椭圆
在椭圆![]() 上,结合已知,即可求得答案.
上,结合已知,即可求得答案.
(1)![]() 椭圆
椭圆![]() :
:![]() ,过椭圆右焦点的最短弦长是
,过椭圆右焦点的最短弦长是![]()
![]()
![]() ,即
,即![]()
![]() ①
①
![]() 点
点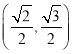 在椭圆上
在椭圆上
![]()
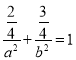 即
即![]()
![]() ②
②
由①②解得: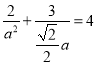 ,
,
![]() 化简可得:
化简可得:![]()
解得![]() ,
,![]() ,
,![]() ,
,
![]() 椭圆的标准方程为
椭圆的标准方程为![]() :
:![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,则由
,则由
![]() 得:
得:![]() ,
,
即![]() ,
,![]() .
.
![]() 点
点![]() ,
,![]() 在椭圆
在椭圆![]() 上,
上,
![]()
![]() ,
,![]() ,
,
故![]()
![]()
![]()
![]() ,
,
设![]() ,
,![]() 分别为直线
分别为直线![]() ,
,![]() 的斜率,
的斜率,
由题设条件知:![]() ,可得
,可得![]() ,
,
![]()
![]() ,
,
![]()
![]() 点是椭圆
点是椭圆![]() 上的点,设该椭圆的左、右焦点为点
上的点,设该椭圆的左、右焦点为点![]() ,
,![]() ,
,
使得![]() 为定值
为定值![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目