Question

【题目】设数列的前项和，对任意，都有（为常数）.

（1）当时，求；

（2）当时，

（ⅰ）求证：数列是等差数列；

（ⅱ）若数列为递增数列且，设，试问是否存在正整数（其中），使成等比数列？若存在，求出所有满足条件的数组；若不存在，说明理由.

Answer 1

【答案】（1）（2）（ⅰ）证明见解析（ⅱ）存在唯一正整数数对，使成等比数列

【解析】

（1）当时，利用公式计算得到，再计算得到.

（2）（ⅰ）化简得到，得到，化简得到

得到答案.

（2）（ⅱ）计算，假设存在正整数数组，则当，且时，，故数列为递减数列，为方程的一组解，得到答案.

（1）时，①

时，②

由②－①得即

时，，∴

（常数，），∴以1为首项，4为公比的等比数列

∴

（2）（ⅰ）当，，时，.③

当时，.④

③－④得：，⑤

所以.⑥

⑤－⑥得：.

因为，所以，即，

所以是等差数列.

（ⅱ）因为为递增等差数列.，又

得或者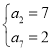（舍），所以

假设存在正整数数组，使成等比数列，则成等差数列，

于是，

所以，（☆）

易知为方程（☆）的一组解.

当，且时，，故数列为递减数列，

于是，所以此时方程（☆）无正整数解.

综上，存在唯一正整数数对，使成等比数列.