题目内容
已知抛物线 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
.
(I)求 与
与 的值;
的值;
(II)设抛物线 上一点
上一点 的横坐标为
的横坐标为 ,过
,过 的直线交
的直线交 于另一点
于另一点 ,交
,交 轴于点
轴于点 ,过点
,过点 作
作 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求 的最小值.
的最小值.
 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
.(I)求
 与
与 的值;
的值;(II)设抛物线
 上一点
上一点 的横坐标为
的横坐标为 ,过
,过 的直线交
的直线交 于另一点
于另一点 ,交
,交 轴于点
轴于点 ,过点
,过点 作
作 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求 的最小值.
的最小值.(Ⅰ)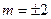 ;(Ⅱ)
;(Ⅱ)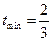
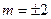 ;(Ⅱ)
;(Ⅱ)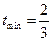
解:(Ⅰ)由抛物线方程得其准线方程: ,根据抛物线定义:点
,根据抛物线定义:点 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即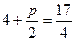 ,解得
,解得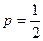
 抛物线方程为:
抛物线方程为: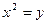 ,将
,将 代入抛物线方程,解得
代入抛物线方程,解得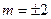
(Ⅱ)由题意知,过点 的直线
的直线 斜率存在且不为0,设其为
斜率存在且不为0,设其为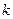 。
。
则 ,当
,当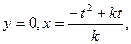 则
则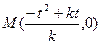 。
。
联立方程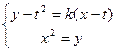 ,整理得:
,整理得: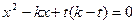
即: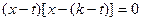 ,解得
,解得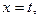 或
或
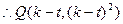 ,而
,而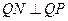 ,
, 直线
直线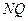 斜率为
斜率为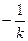
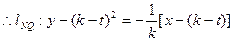 ,联立方程
,联立方程
整理得: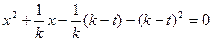 ,即:
,即:
 ,解得:
,解得: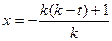 ,或
,或
 ,
,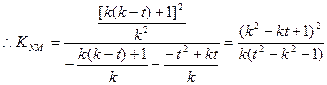
而抛物线在点N处切线斜率:
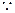 MN是抛物线的切线,
MN是抛物线的切线, ,整理得
,整理得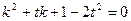
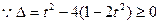 ,解得
,解得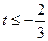 (舍去),或
(舍去),或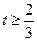 ,
,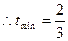


 ,根据抛物线定义:点
,根据抛物线定义:点 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即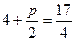 ,解得
,解得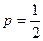
 抛物线方程为:
抛物线方程为: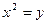 ,将
,将 代入抛物线方程,解得
代入抛物线方程,解得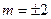
(Ⅱ)由题意知,过点
 的直线
的直线 斜率存在且不为0,设其为
斜率存在且不为0,设其为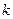 。
。则
 ,当
,当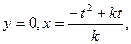 则
则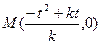 。
。联立方程
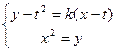 ,整理得:
,整理得: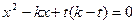
即:
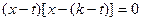 ,解得
,解得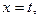 或
或
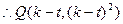 ,而
,而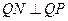 ,
, 直线
直线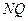 斜率为
斜率为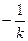
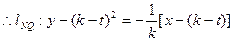 ,联立方程
,联立方程
整理得:
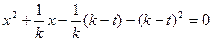 ,即:
,即:
 ,解得:
,解得: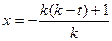 ,或
,或
 ,
,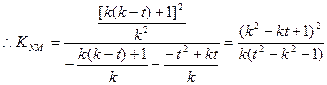
而抛物线在点N处切线斜率:

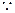 MN是抛物线的切线,
MN是抛物线的切线, ,整理得
,整理得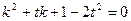
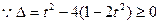 ,解得
,解得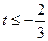 (舍去),或
(舍去),或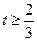 ,
,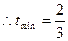



练习册系列答案
相关题目
 ,它的离心率为
,它的离心率为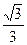 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,线段
,线段 的垂直平分线交
的垂直平分线交 ,求动点
,求动点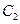 的方程;⑶将曲线
的方程;⑶将曲线 ,设曲线
,设曲线 ,焦点为
,焦点为 ,过
,过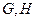 两点,过点
两点,过点 作平行于曲线
作平行于曲线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上. . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明. .
. 是定值;
是定值; ,求椭圆的离心率;
,求椭圆的离心率; ,求椭圆的方程.
,求椭圆的方程.
 ,
, 且有
且有 ,则
,则 点的轨迹是( )
点的轨迹是( )