题目内容

16．P为边长为2的正三角形内（不包括边界）一点，P到三角形三边距离分别为a、b、c，则ab+bc+ca取值范围是（　　）
A．（0，1]B．（0，2）C．$（{0，2\sqrt{3}}）$D．（0，4）

分析 根据三角形的面积公式，和基本不等式即可求出

解答 解：∵$\frac{1}{2}$×2×（a+b+c）=$\frac{1}{2}$×2×$\sqrt{3}$，
∴a+b+c=$\sqrt{3}$．
∵（a+b+c）2≥3（ab+ac+bc），当且仅当a=b=c=$\frac{\sqrt{3}}{3}$取等号，
∴ab+bc+ca≤1．
又ab+bc+ca＞0．
∴ab+bc+ca的取值范围是（0，1]．
故选：A．

点评 本题考查了等边三角形的面积计算公式、不等式的性质，考查了推理能力和计算能力，属于中档题．

练习册系列答案
相关题目
6．如果实数x，y满足x2+y2=4，那么$\frac{y-2}{x+3}$的最小值是（　　）
A．-$\frac{12}{5}$B．-1C．-$\frac{5}{12}$D．0
7．已知$a={log_3}\frac{1}{2}，b={2^{0.01}}，c=ln\frac{1}{2}$，则a，b，c的大小关系为（　　）
A．b＞a＞cB．b＞c＞aC．a＞c＞bD．a＞b＞c
4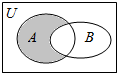．设全集为U=R，集合A={x|（x+3）（x-6）≤0}，B={x|log2（x+2）＜4}．
（1）求如图阴影部分表示的集合；
（2）已知C={x|2a＜x＜a+1}，若C⊆B，求实数a的取值范围．
11．已知集合A={1，2}，B={x|x2=1}，则A∪B={-1，1，2}．
1．在复平面内，复数（4+5i）i（i为虚数单位）的共轭复数对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
8．（1）化简：（$\frac{b}{2{a}^{2}}$）${\;}^{3}÷（\frac{2{b}^{2}}{3a}）^{0}×（-\frac{b}{a}）^{-3}$；
（2）若a＞0，b＞0，化简：$\frac{（2{a}^{\frac{2}{3}}{b}^{\frac{1}{2}}）•（-6{a}^{\frac{1}{2}}{b}^{\frac{1}{3}}）}{-3{a}^{\frac{1}{6}}{b}^{\frac{5}{6}}}-（4a-1）$．
5．已知圆C的方程为x2+（y-4）2=4，点O是坐标原点，直线l：y=kx与圆C交于M，N两点．
（1）求k的取值范围；
（2）求弦MN中点G的轨迹方程，并求出轨迹的长度；
（3）设Q（m，n）是线段MN上的点，且$\frac{2}{{|OQ{|^2}}}=\frac{1}{{|OM{|^2}}}+\frac{1}{{|ON{|^2}}}$，请将n表示为m的函数，并求其定义域．
6．已知A={α|sinα≤$\frac{\sqrt{2}}{2}$，α∈[0，2π）}，B={β|cosβ≤$\frac{\sqrt{2}}{2}$，β∈[0，2π）}，则A∩B=$\{\frac{π}{4}\}$∪$[\frac{3π}{4}，\frac{7π}{4}]$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网