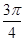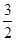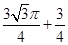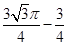题目内容
设f(x)=- x3+
x3+ x2+2ax.
x2+2ax.
(1)若f(x)在( ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为- ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
 x3+
x3+ x2+2ax.
x2+2ax.(1)若f(x)在(
 ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.(2)当0<a<2时,f(x)在[1,4]上的最小值为-
 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.(1) a>- (2) f(x)max=
(2) f(x)max=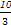
 (2) f(x)max=
(2) f(x)max=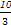
(1)f(x)=- x3+
x3+ x2+2ax,
x2+2ax,
∴f'(x)=-x2+x+2a,当x∈[ ,+∞)时,f'(x)的最大值为f'(
,+∞)时,f'(x)的最大值为f'( )=
)= +2a.
+2a.
函数f(x)在( ,+∞)上存在单调递增区间,即导函数在(
,+∞)上存在单调递增区间,即导函数在( ,+∞)上存在函数值大于零成立,
,+∞)上存在函数值大于零成立,
∴ +2a>0
+2a>0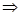 a>-
a>- .
.
(2)已知0<a<2,f(x)在[1,4]上取到最小值- ,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x=
,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x= ,
,
∴f'(1)=-1+1+2a=2a>0,
f'(4)=-16+4+2a=2a-12<0,
则必有一点x0∈[1,4]使得f'(x0)=0,此时函数f(x)在[1,x0]上单调递增,在[x0,4]上单调递减,
f(1)=- +
+ +2a=
+2a= +2a>0,
+2a>0,
∴f(4)=- ×64+
×64+ ×16+8a=-
×16+8a=-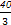 +8a,
+8a,
∴-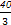 +8a=-
+8a=- ,得a=1,
,得a=1,
此时,由f'(x0)=-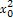 +x0+2=0得x0=2或-1(舍去),
+x0+2=0得x0=2或-1(舍去),
所以函数f(x)max=f(2)=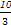 .
.
 x3+
x3+ x2+2ax,
x2+2ax,∴f'(x)=-x2+x+2a,当x∈[
 ,+∞)时,f'(x)的最大值为f'(
,+∞)时,f'(x)的最大值为f'( )=
)= +2a.
+2a.函数f(x)在(
 ,+∞)上存在单调递增区间,即导函数在(
,+∞)上存在单调递增区间,即导函数在( ,+∞)上存在函数值大于零成立,
,+∞)上存在函数值大于零成立,∴
 +2a>0
+2a>0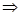 a>-
a>- .
.(2)已知0<a<2,f(x)在[1,4]上取到最小值-
 ,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x=
,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x= ,
,∴f'(1)=-1+1+2a=2a>0,
f'(4)=-16+4+2a=2a-12<0,
则必有一点x0∈[1,4]使得f'(x0)=0,此时函数f(x)在[1,x0]上单调递增,在[x0,4]上单调递减,
f(1)=-
 +
+ +2a=
+2a= +2a>0,
+2a>0,∴f(4)=-
 ×64+
×64+ ×16+8a=-
×16+8a=-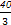 +8a,
+8a,∴-
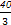 +8a=-
+8a=- ,得a=1,
,得a=1,此时,由f'(x0)=-
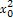 +x0+2=0得x0=2或-1(舍去),
+x0+2=0得x0=2或-1(舍去),所以函数f(x)max=f(2)=
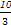 .
.
练习册系列答案
相关题目
 .
. 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;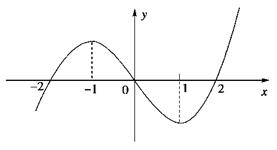
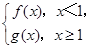 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.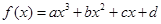 在
在 ,
,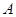 点处取到极值,其中
点处取到极值,其中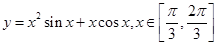 上,则曲线
上,则曲线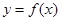 的切线的斜率的最大值是( )
的切线的斜率的最大值是( )