题目内容
已知函数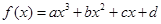 在
在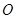 ,
,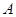 点处取到极值,其中
点处取到极值,其中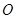 是坐标原点,
是坐标原点,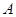 在曲线
在曲线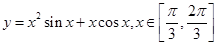 上,则曲线
上,则曲线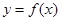 的切线的斜率的最大值是( )
的切线的斜率的最大值是( )
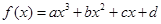 在
在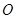 ,
,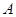 点处取到极值,其中
点处取到极值,其中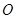 是坐标原点,
是坐标原点,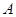 在曲线
在曲线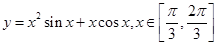 上,则曲线
上,则曲线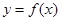 的切线的斜率的最大值是( )
的切线的斜率的最大值是( )A.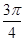 | B.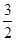 | C.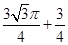 | D.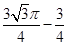 |
A.
试题分析:根据题意由函数
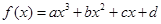 ,
,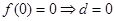 ,则
,则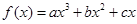 ,设
,设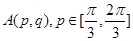 ,由
,由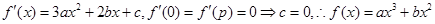 ,又有
,又有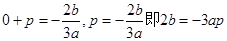 ,
,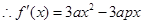 ,又
,又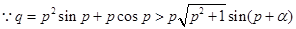 ,其中
,其中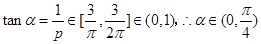 ,则有
,则有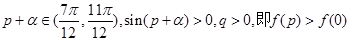 ,所以
,所以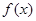 分别在
分别在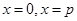 处取得极小值和极大值,则
处取得极小值和极大值,则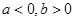 ,
,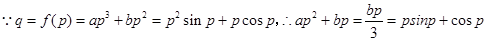 ,
,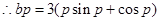 ,
,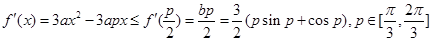 ,令
,令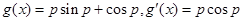 ,由
,由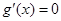 得
得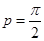 ,
,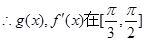 上单调递增,在
上单调递增,在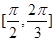 上单调递减,所以
上单调递减,所以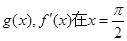 处取得唯一极大值,即最大值,所以
处取得唯一极大值,即最大值,所以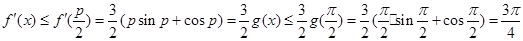 .
.
练习册系列答案
相关题目
 .
. ;
; 时,
时, ,求
,求 的取值范围.
的取值范围.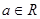 ,函数
,函数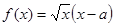 .
.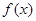 的单调区间;
的单调区间;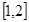 上的最小值.
上的最小值. ,过曲线
,过曲线 上的点
上的点 的切线方程为
的切线方程为 .
.  时有极值,求
时有极值,求 的表达式;
的表达式;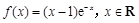 ,其中
,其中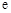 是自然对数的底数.
是自然对数的底数.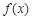 的单调区间和极值;
的单调区间和极值;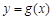 对任意
对任意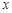 满足
满足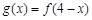 ,求证:当
,求证:当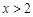 时,
时,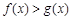 ;
;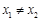 ,且
,且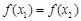 ,求证:
,求证: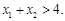
 x3+
x3+ x2+2ax.
x2+2ax. ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围. ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.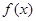 ,对任意x都有
,对任意x都有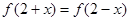 ,且其导函数
,且其导函数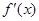 满足
满足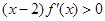 ,则当
,则当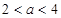 时,有( )
时,有( )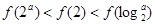
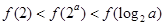
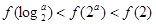
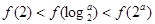
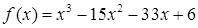 的单调减区间为 .
的单调减区间为 .