题目内容
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
 .
.(1)若函数
 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;(2)当a=1时,求函数
 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.(1)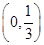 (2)
(2)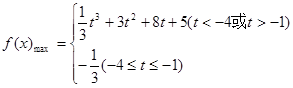
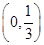 (2)
(2)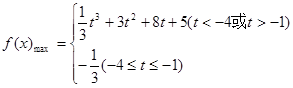
试题分析:
(1)根据题意对函数
 求导,获得导函数
求导,获得导函数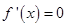 的根与大于0小于0的解集,获得函数
的根与大于0小于0的解集,获得函数 的单调区间和极值点,极值.进而确定函数
的单调区间和极值点,极值.进而确定函数 在区间
在区间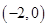 上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在
上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在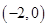 上要有两个零点,需要
上要有两个零点,需要 满足
满足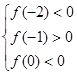 即可,解不等式即可求出
即可,解不等式即可求出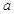 的取值范围.
的取值范围.(2)根据题意
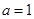 ,则利用(1)可以得到
,则利用(1)可以得到 的单调性以及极值点,极值.要得到函数
的单调性以及极值点,极值.要得到函数 在含参数的区间
在含参数的区间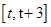 上的最大值,我们需要讨论
上的最大值,我们需要讨论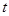 的范围得到函数
的范围得到函数 的在区间
的在区间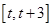 上的单调性进而得到
上的单调性进而得到 在该区间上的最大值,为此分三种情况分别为
在该区间上的最大值,为此分三种情况分别为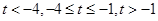 ,依次确定单调性得到最大值即可.
,依次确定单调性得到最大值即可.试题解析:
(1)∵

∴
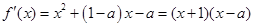 , (1分)
, (1分)令
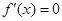 ,解得
,解得 (2分)
(2分)当x变化时,
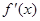 ,
, 的变化情况如下表:
的变化情况如下表: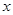 | 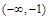 | 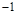 | 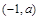 | 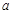 | 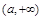 |
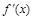 | 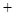 | 0 | — | 0 | 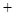 |
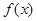 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 的单调递增区间为(-∞,-1),(a,+∞);单调递减区间为(-1,a);(4分)
的单调递增区间为(-∞,-1),(a,+∞);单调递减区间为(-1,a);(4分)因此
 在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,要使函数
在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,要使函数 在区间
在区间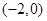 内恰有两个零点,当且仅当
内恰有两个零点,当且仅当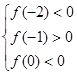 , (5分)
, (5分)解得
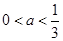 , 所以a的取值范围是(0,
, 所以a的取值范围是(0,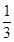 ). (6分)
). (6分)(2)当a=1时,
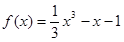 . 由(1)可知,函数
. 由(1)可知,函数 的单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,1);
的单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,1);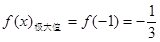 . (7分)
. (7分)①当t+3<-1,即t<-4时,
因为
 在区间[t,t+3]上单调递增,所以
在区间[t,t+3]上单调递增,所以 在区间[t,t+3]上的最大值为
在区间[t,t+3]上的最大值为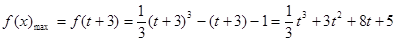 ; (9分)
; (9分)②当
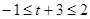 ,即
,即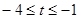 时,
时,因为
 在区间
在区间 上单调递增,在区间[-1,1]上单调递减,在区间[1,2]上单调递增,且
上单调递增,在区间[-1,1]上单调递减,在区间[1,2]上单调递增,且 ,所以
,所以 在区间
在区间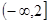 上的最大值为
上的最大值为 . (10分)
. (10分)由
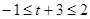 ,即
,即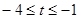 时,有[t,t+3]Ì
时,有[t,t+3]Ì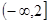 ,-1Î[t,t+3],所以
,-1Î[t,t+3],所以 在
在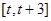 上的最大值为
上的最大值为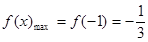 ; (11分)
; (11分)③当t+3>2,即t>-1时,
由②得
 在区间
在区间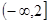 上的最大值为
上的最大值为 .
. 因为
 在区间(1,+∞)上单调递增,所以
在区间(1,+∞)上单调递增,所以 ,
,故
 在
在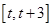 上的最大值为
上的最大值为 . (13分)
. (13分)综上所述,当a=1时,
 在[t,t+3]上的最大值
在[t,t+3]上的最大值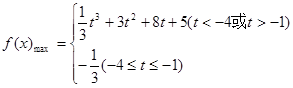 . (14分)
. (14分)
练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 .
. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数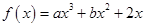 在
在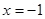 处取得极值,且在点
处取得极值,且在点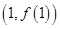 处的切线斜率为
处的切线斜率为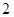 .
.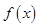 的单调增区间;
的单调增区间;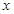 的方程
的方程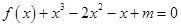 在区间
在区间 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围.
的取值范围. x2
x2 ㏑x的单调递减区间为( )
㏑x的单调递减区间为( ) 1,1]
1,1] 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数 的导函数).下面四个图象中,
的导函数).下面四个图象中, 的图象大致是( )
的图象大致是( )

 在
在 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )



 x2-mlnx+(m-1)x,当m≤0时,试讨论函数f(x)的单调性;
x2-mlnx+(m-1)x,当m≤0时,试讨论函数f(x)的单调性; x3+
x3+ x2+2ax.
x2+2ax. ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围. ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.