Question

【题目】（题文）

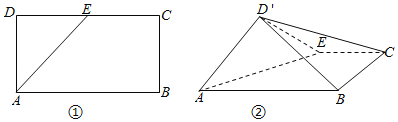
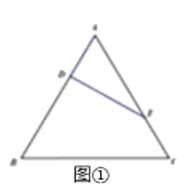
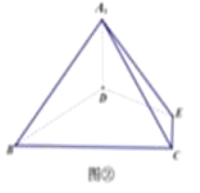
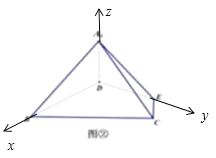
等边△ABC的边长为3，点D，E分别为AB，AC上的点，且满足（如图①），将△ADE沿DE折起到△A1DE的位置，使二面角A1﹣DE﹣B成直二面角，连接A1B，A1C（如图②）.

（1）求证：A1D⊥平面BCED；

（2）在线段BC上是否存在点P（不包括端点），使直线PA1与平面A1BD所成的角为60°？若存在，求出A1P的长，若不存在，请说明理由.

Answer 1

【答案】（1）证明见解析（2）存在；A1P

【解析】

（1）计算，利用勾股定理可证A1D⊥DE，再根据面面垂直的性质得出平面；

（2）建立空间坐标系，设，求出平面的法向量，根据线面角列方程计算的值即可得出结论．

（1）证明：由题意可知A1D＝1，A1E＝2，∠DAE＝60°，

∴DE，

∴A1D2+DE2＝A1E2，∴A1D⊥DE，

∵二面角A1﹣DE﹣B成直二面角，即平面A1DE⊥平面BDE，平面A1DE∩平面BDE＝DE，

∴A1D⊥平面BCED.

（2）由（1）可知DE⊥BD，

以D为原点，以DB，DE，DA1为坐标轴建立空间坐标系D﹣xyz，如图所示，

则D（0，0，0），B（2，0，0），A1（0，0，1），C（，，0），

则（，，0），（2，0，0），令（0＜λ＜1），

则（2λ，λ，0），即P（2λ，λ，0），

∴（2λ，λ，﹣1），

由（1）知（0，1，0）为平面A1BD的一个法向量，

则cos，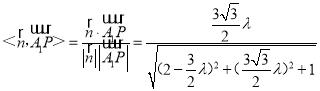

令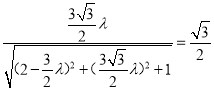，解得λ，即（，，﹣1），

∴A1P.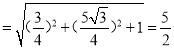

∴线段BC上存在点P使得直线PA1与平面A1BD所成的角为60°，且A1P.