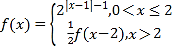题目内容
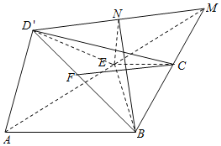
【题目】如图①,在矩形ABCD中,AB=2,BC=1,E是CD的中点,将三角形ADE沿AE翻折到图②的位置,使得平面AED′⊥平面ABC.
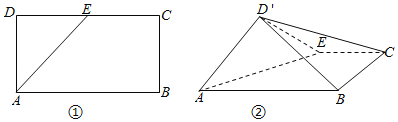
(1)在线段BD'上确定点F,使得CF∥平面AED',并证明;
(2)求△AED'与△BCD'所在平面构成的锐二面角的正切值.
【答案】(1)点F是线段BD'的中点,见解析(2)![]() .
.
【解析】
(1)取BD'的中点![]() ,记AE,BC延长线交于点M,由平面几何知识可得点C是BM的中点,可得CF∥MD',可得CF∥平面AED';
,记AE,BC延长线交于点M,由平面几何知识可得点C是BM的中点,可得CF∥MD',可得CF∥平面AED';
(2)先根据面面垂直的性质可得BE⊥平面AED',在平面AED'内作EN⊥MD',可得∠BNE就是△AED'与△BCD'所在平面构成的锐二面角的平面角,最后解三角形可得锐二面角的正切值.
(1)点F是线段BD'的中点时,CF∥平面AED'.
证明:记AE,BC延长线交于点M,
∵AB=2EC,∴点C是BM的中点,
∴CF∥MD',而MD'在平面AED'内,CF在平面AED'外,
∴CF∥平面AED';
(2)在矩形ABCD中,AB=2,CD=1,BE⊥AE,
∵平面AED'⊥平面ABC,且交线是AE,∴BE⊥平面AED',
在平面AED'内作EN⊥MD',连接BN,则BN⊥MD′.
∴∠BNE就是△AED'与△BCD'所在平面构成的锐二面角的平面角,
求解三角形可得![]() ,
,![]() ,
,
∴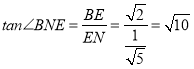 .
.

练习册系列答案
相关题目