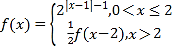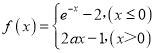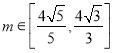Question

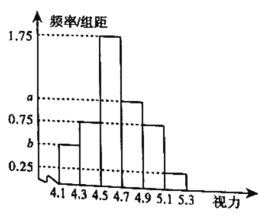
【题目】对某校高三年级100名学生的视力情况进行统计（如果两眼视力不同，取较低者统计），得到如图所示的频率分布直方图，已知从这100人中随机抽取1人，其视力在的概率为.

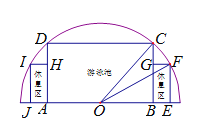
（1）求a，b的值；

（2）若报考高校A专业的资格为：任何一眼裸眼视力不低于5.0，已知在中有的学生裸眼视力不低于5.0.现用分层抽样的方法从和中抽取4名同学，设这4人中有资格（仅考虑视力）考A专业的人数为随机变量ξ，求ξ的分布列及数学期望.

Answer 1

【答案】（1）；（2）分布列见解析，期望值为.

【解析】

（1）根据“从这100人中随机抽取1人，其视力在的概率为”求得，根据频率之和为列方程求得.

（2）首先求得和中分别抽取的人数，再按照分布列的计算方法求得分布列并求得数学期望.

（1）由于“从这100人中随机抽取1人，其视力在的概率为”所以.由，解得.

（2）和的频率比为，所以在中抽取人，在中抽取人. 的人数为，其中视力以上有人，视力以下有人.的人数为人.的所有可能取值为，且

，，，.所以分布列为

	1	2	3	4

所以.