Question

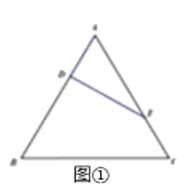
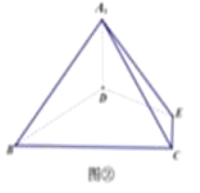
【题目】在三棱锥A﹣BCD中，∠ABC＝∠ABD＝∠CBD＝90°，BC＝BD＝BA＝1，过点A作平面α与BC，BD分别交于P，Q两点，若AB与平面α所成的角为30°，则截面APQ面积的最小值是（ ）

A.1B.C.D.

Answer 1

【答案】B

【解析】

由题意画出图形，求得A到PQ的距离为定值，然后求PQ的最小值，代入三角形面积公式得答案．

过B作BO⊥PQ，垂足为O，连接AO，如下图所示：

∵AB⊥BC，AB⊥BD，BC∩BD＝B，∴AB⊥PQ，

又BO⊥PQ，且AB∩BO＝B，∴PQ⊥平面ABO，则PQ⊥AO，

则∠BAO为AB与平面α所成的角为30°，

∵AB＝1，∴AO＝为定值．

要使截面APQ面积最小，则PQ最小，此时BO⊥PQ，

PQ的最小值为．

∴截面APQ面积的最小值是S＝．

故选：B