题目内容
10.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(φ>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如下表:| φx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | ||
| Asin(φx+φ) | 0 | 3 | 0 | -3 | 0 |
(Ⅱ)将y=f(x)图象上所有点向右平行移动$\frac{π}{3}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离y轴最近的对称轴.
分析 (Ⅰ)根据用五点法作函数y=Asin(ωx+φ)在一个周期上的图象的方法,将上表数据补充完整,直接写出函数f(x)的解析式.
(Ⅱ)由条件利用y=Asin(ωx+φ)的图象变换规律,以及正弦函数的图象的对称性,得出结论.
解答 解:(Ⅰ)根据表中已知数据可得:A=3,$(-\frac{π}{6})ω+φ=0$,$\frac{π}{3}ω+φ=π$,
解得 $ω=2,φ=\frac{π}{3}$,数据补全如下表:
| φx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $-\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| Asin(φx+φ) | 0 | 3 | 0 | -3 | 0 |
(Ⅱ)由(Ⅰ)知$f(x)=3sin(2x+\frac{π}{3})$,将y=f(x)图象上所有点向右平行移动$\frac{π}{3}$个单位长度,
可得$g(x)=3sin[2(x-\frac{π}{3})+\frac{π}{3}]=3sin(2x-\frac{π}{3})$,
因为y=sinx的对称轴是$x=kπ+\frac{π}{2}$,k∈Z,
令$2x-\frac{π}{3}=kπ+\frac{π}{2}$,解得$x=\frac{kπ}{2}+\frac{5π}{12},k∈Z$,令k=-1,可得$x=-\frac{π}{12}$,
所以y=g(x)的图象离y轴最近的对称轴$x=-\frac{π}{12}$.
点评 本题主要考查用五点法作函数y=Asin(ωx+φ)在一个周期上的图象,利用了y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于中档题.

练习册系列答案
相关题目
1.设命题p:函数f(x)=x3在R上为增函数;命题q:函数f(x)=cosx为奇函数.则下列命题中真命题是( )
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
19.设集合A={0,3},B={a,1},若A∩B={0},则A∪B=( )
| A. | {a,0,1,3} | B. | {0,1,3} | C. | {1,3} | D. | {0} |
5.设函数f(x)=$\left\{\begin{array}{l}{{2}^{1-x},x≤1}\\{1-lo{g}_{2}x,x>1}\end{array}\right.$,则f(f(8))=8.
15.已知函数y=ex,若f(x)的图象的一条切线经过点(-1,0),则这条切线与直线x=2及x轴所围成的三角形面积为( )
| A. | $\frac{4}{e}$ | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{{e}^{2}}{2}$ |
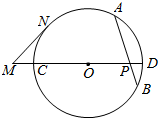 如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.
如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.