题目内容
【题目】椭圆
（
）的离心率是
，点
在短轴
上，且
。
（1）球椭圆
的方程；
（2）设
为坐标原点，过点
的动直线与椭圆交于
两点。是否存在常数
，使得
为定值？若存在，求
的值；若不存在，请说明理由。
【答案】（1）
；（2）见解析.
【解析】（Ⅰ）由已知，点C，D的坐标分别为（0，－b），（0，b）
又点P的坐标为（0，1），且
＝－1
于是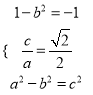
，解得a＝2，b＝
所以椭圆E方程为
.
（Ⅱ）当直线AB斜率存在时，设直线AB的方程为y＝kx＋1
A，B的坐标分别为（x1，y1），（x2，y2）
联立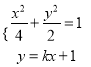
，得（2k2＋1）x2＋4kx－2＝0
其判别式△＝（4k）2＋8（2k2＋1）＞0
所以
从而
＝x1x2＋y1y2＋λ[x1x2＋（y1－1）（y2－1）]
＝（1＋λ）（1＋k2）x1x2＋k（x1＋x2）＋1
＝
＝－
所以，当λ＝1时，－＝－3
此时， 
＝－3为定值
当直线AB斜率不存在时，直线AB即为直线CD
此时
＝－2－1＝－3
故存在常数λ＝－1，使得
为定值－3.
练习册系列答案
相关题目
