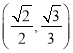题目内容
【题目】如图，在直三棱柱ABC﹣A1B1C1（侧棱垂直于底面的棱柱为直棱柱）中，BC=CC1=1，AC=2，∠ABC=90°． 
（1）求证：平面ABC1⊥平面A1B1C；
（2）设D为AC的中点，求平面ABC1与平面C1BD所成锐角的余弦值．
【答案】
（1）证明：∵直三棱柱ABC﹣A1B1C1，BC=CC1，
∴四边形BCC1B1是正方形，
∴BC1⊥B1C，
∵AB⊥BC，AB⊥BB1，BC，BB1平面BCC1B1，BC∩BB1=B，
∴AB⊥平面BCC1B1，∵BC1平面BCC1B1，
∴AB⊥BC1，又∵AB∥A1B1，
∴A1B1⊥BC1，又A1B1平面平面A1B1C，B1C平面A1B1C，A1B1∩B1C=B1，
∴BC1⊥平面A1B1C，又BC1平面ABC1，
∴平面ABC1⊥平面A1B1C．
（2）证明：∵BC=CC1=1，AC=2，∠ABC=90°．
∴AB= 
，
建立以B为坐标原点，BC，BA，BB1分别为x，y，z轴的空间直角坐标系如图：
则B（0，0，0），C（1，0，0），B1（0，0，1），A（0， ，0），C1（1，0，1），D（ 
， 
，0），
设平面ABC1的法向量为 
=（x，y，z），
则 
=（1，0，1）， 
=（0， ，0），
则 =x+z=0， = y=0，
令x=1，则z=﹣1，y=0，即平面ABC1的法向量为， =（1，0，﹣1），
设平面C1BD的法向量为 
=（x，y，z），
则 =（1，0，1）， 
=（ ， ，0），
则 =x+z=0， = x+ y=0，
令y=1，则x=﹣ ，z= ，即平面C1BD的法向量为， =（﹣ ，1， ），
则 
= 
= 
= 
=﹣ 
则平面ABC1与平面C1BD所成锐角的余弦值是 ．
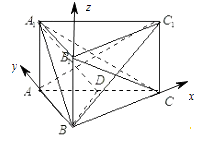
【解析】（1）由四边形BCC1B1是正方形得BC1⊥B1C，由A1B1⊥平面BCC1B1得出A1B1⊥BC1 ， 故BC1⊥平面A1B1C，从而平面ABC1⊥平面A1B1C；（2）建立空间坐标系，求出平面的法向量，利用向量法即可平面ABC1与平面C1BD所成锐角的余弦值．
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．
