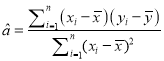题目内容
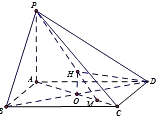
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠BAD=120°,对角线AC与BD交于点O,M为OC中点. 
(1)求证:BD⊥PM
(2)若二面角O﹣PM﹣D的正切值为2 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)证明:∵四棱锥P﹣ABCD中,PA⊥平面ABCD,
又BD平面ABCD,∴BD⊥PA,
∵底面ABCD是菱形,
∴BD⊥AC,
又PA∩AC=A,∴BD⊥平面PAC,
又PM平面PAC,
∴BD⊥PM.
(2)解:过O作OH⊥PM交PM于H,连HD,
因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,
所以∠OHD为A﹣PM﹣D的平面角,
设PA=b,AD=4,
∵底面ABCD是边长为4的菱形,∠BAD=120°,
∴OD=2 ![]() ,OM=1,AM=3,且
,OM=1,AM=3,且 ![]() =
= ![]() ,
,
从而OH= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠OHD= ![]() =
= ![]() ,
,
所以16b2=144,解得b=3.(舍负值)
∴PA的长为3.
则 ![]() =
= ![]() .
.
【解析】(1)根据线面垂直的判定,先证明BD⊥平面PAC,利用线面垂直的性质即可证明BD⊥PM.(2)过O作OH⊥PM交PM于H,连HD,则∠OHD为A﹣PM﹣D的平面角,利用二面角O﹣PM﹣D的正切值为2 ![]() ,即可求出
,即可求出 ![]() 的值.
的值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

【题目】某企业为了对新研发的一批产品进行合理定价,将产品按事先拟定的价格进行试销,得到一组销售数据![]() 2,
2,![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | 90 | 84 | 83 | 80 | q | 68 |
已知![]() .
.
![]() 求表格中q的值;
求表格中q的值;
![]() 已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程
已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程![]() 参考数据
参考数据![]() ;
;
![]() 用
用![]() 中的回归方程得到的与
中的回归方程得到的与![]() 对应的产品销量的估计值记为
对应的产品销量的估计值记为![]() 2,
2,![]() ,
,![]() 当
当![]() 时,则称
时,则称![]() 为一个“理想数据”
为一个“理想数据”![]() 试确定销售单价分别为4,5,6时有哪些是“理想数据”.
试确定销售单价分别为4,5,6时有哪些是“理想数据”.