题目内容
【题目】某集团公司计划从甲分公司中的3位员工
、
、
和乙分公司中的3位员工
、
、
选择2位员工去国外工作.
（1）若从这6名员工中任选2名，求这2名员工都是甲分公司的概率；
（2）若从甲分公司和乙分公司中各任选1名员工，求这2名员工包括但不包括的概率.
【答案】（1）
； （2）
.
【解析】
（1）从这6名员工中任选2个，基本事件一一列出，总共有15个，这两名员工都是甲分公司的基本事件为3，利用公式求得概率；
（2）从甲分公司和乙分公司中各任选1名员工，用列举法找出其对应的基本事件，共2个，利用公式求得概率.
（1）由题意得，从6名员工中任选2名，其一切可能的结果组成的基本事件有：
，共15个
所选两名员工都是甲分公司所包含的基本事件有：
，共3个，
所以所求事件的概率为
；
（2）从甲分公司和乙分公司各任选1名员工，其一切可能的结果组成的基本事件有： 
共9个，包含
但不包括
的事件所包含的基本事件有
，
共2个，所以所求事件的概率为
【题目】已知从甲地到乙地的公路里程约为240（单位：km）.某汽车每小时耗油量Q（单位：L）与速度x（单位：
）（
）的关系近似符合以下两种函数模型中的一种（假定速度大小恒定）：①
，②
，经多次检验得到以下一组数据：
x | 0 | 40 | 60 | 120 |
Q | 0 |
|
| 20 |
（1）你认为哪一个是符合实际的函数模型，请说明理由；
（2）从甲地到乙地，这辆车应以多少速度行驶才能使总耗油量最少？
【题目】某高校在2012年的自主招生考试成绩中随机抽取
名中学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
（1）请先求出频率分布表中
位置的相应数据，再完成频率分布直方图；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第
组中用分层抽样抽取名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试；
（3）在（2）的前提下，学校决定在
名学生中随机抽取
名学生接受
考官进行面试，求：第
组至少有一名学生被考官面试的概率．
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据
|
|
|
|
|
|
|
|
|
|
（1）请根据上表提供的数据，用最小二乘法求出关于
的线性回归方程
；
（2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(附:
，
，
，
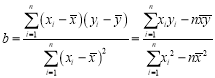，其中
,
为样本平均值)
