题目内容
9.在平面直角坐标系中,已知椭圆C:$\frac{x^2}{24}+\frac{{y{\;}^2}}{12}$=1,设R(x0,y0)是椭圆C上任一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,切点分别为P,Q.(1)若直线OP,OQ互相垂直,且R在第一象限,求圆R的方程;
(2)若直线OP,OQ的斜率都存在,并记为k1,k2,求证:2k1k2+1=0.
分析 (1)由直线OP,OQ互相垂直,且与圆R相切,可得OR=4,再由R在椭圆上,满足椭圆方程,求得点R的坐标,即可得到圆R的方程;
(2)运用直线和圆相切的条件:d=r,结合二次方程的韦达定理和点R满足椭圆方程,化简整理,即可得证.
解答 解:(1)由题圆R的半径为$2\sqrt{2}$,因为直线OP,OQ互相垂直,且与圆R相切,
所以$OR=\sqrt{2}r=4$,即${x_0}^2+{y_0}^2=16$,①
又R(x0,y0)在椭圆C上,所以$\frac{{{x_0}^2}}{24}+\frac{{{y_0}{\;}^2}}{12}=1$,②
由①②及R在第一象限,解得${x_0}={y_0}=2\sqrt{2}$,
所以圆R的方程为:${({x-2\sqrt{2}})^2}+{({y-2\sqrt{2}})^2}=8$;
(2)证明:因为直线OP:y=k1x,OQ:y=k2x均与圆R相切,
所以$\frac{{|{{k_1}{x_0}-{y_0}}|}}{{\sqrt{1+{k_1}^2}}}=2\sqrt{2}$,化简得$({x_0}^2-8){k_1}^2-2{x_0}{y_0}{k_1}+{y_0}^2-8=0$,
同理有$({x_0}^2-8){k_2}^2-2{x_0}{y_0}{k_2}+{y_0}^2-8=0$,
所以k1,k2是方程$({x_0}^2-8){k^2}-2{x_0}{y_0}k+{y_0}^2-8=0$的两个不相等的实数根,
所以${k_1}{k_2}=\frac{{{y_0}^2-8}}{{{x_0}^2-8}}$.又因为R(x0,y0)在椭圆C上,所以$\frac{{{x_0}^2}}{24}+\frac{{{y_0}{\;}^2}}{12}=1$,
即${y_0}^2=12-\frac{1}{2}{x_0}^2$,所以${k_1}{k_2}=\frac{{4-\frac{1}{2}{x_0}^2}}{{{x_0}^2-8}}=-\frac{1}{2}$,
即2k1k2+1=0.
点评 本题考查椭圆的方程和运用,同时考查直线和圆相切的条件,以及韦达定理的运用,考查运算化简能力,属于中档题.

 目标测试系列答案
目标测试系列答案| A. | 14个 | B. | 15个 | C. | 16个 | D. | 17个 |

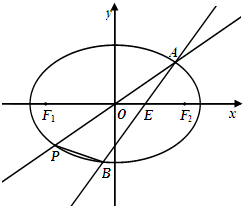 如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.