题目内容
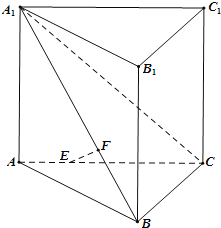
【题目】如图,在直三棱柱![]() 侧棱和底面垂直的棱柱
侧棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,
,![]() ,线段AC、
,线段AC、![]() 上分别有一点E、F且满足
上分别有一点E、F且满足![]() ,
,![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求点E到直线
求点E到直线![]() 的距离;
的距离;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析
(2)![]()
(3)﹣![]()
【解析】
试题(1)过点A在平面A1ABB1内作AD⊥A1B于D,由已知条件推导出AD⊥平面A1BC,由此能证明AB⊥BC.
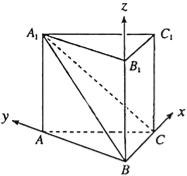
(2)以点B为坐标原点,以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出点E到直线A1B的距离.
(3)分别求出平面BEF的法向量和平面BEC的法向量,利用向量法能求出二面角F﹣BE﹣C的平面角的余弦值.
(1)证明:如图,过点A在平面A1ABB1内作AD⊥A1B于D,
则由平面A1BC⊥侧面A1ABB1,
且平面A1BC∩侧面A1ABB1=A1B,
∴AD⊥平面A1BC,
又∵BC平面A1BC,∴AD⊥BC.
∵三棱柱ABC﹣A1B1C1是直三棱柱,∴AA1⊥底面ABC,∴AA1⊥BC.
又∵AA1∩AD=A,∴BC⊥侧面A1ABB1,
又∵AB侧面A1ABB1,∴AB⊥BC.(4分)
(2)解:由(1)知,以点B为坐标原点,
以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,
B(0,0,0),A(0,3,0),C(3,0,0),A1(0,3,3)
∵线段AC、A1B上分别有一点E、F,满足2AE=EC,2BF=FA1,
∴E(1,2,0),F(0,1,1),
∴![]() ,
,![]() .
.
∵![]() =0,∴EF⊥BA1,
=0,∴EF⊥BA1,
∴点E到直线A1B的距离![]() .(8分)
.(8分)
(3)解:![]() ,
,
设平面BEF的法向量![]() ,
,
则![]() ,取x=2,得
,取x=2,得![]() =(2,﹣1,1),
=(2,﹣1,1),
由题意知平面BEC的法向量![]() ,
,
设二面角F﹣BE﹣C的平面角为θ,
∵θ是钝角,∴cosθ=﹣|cos<![]() >|=﹣
>|=﹣![]() =﹣
=﹣![]() ,
,
∴二面角F﹣BE﹣C的平面角的余弦值为﹣![]() .
.

【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(2)判断该高三学生的记忆力x和判断力是正相关还是负相关;并预测判断力为4的同学的记忆力.
(参考公式: )
)