题目内容

10．已知命题p：?x∈R，2x2+1＞0，则（　　）
A．￢p：?x∈R，2x2+1≤0B．￢p：?x∈R，2x2+1≤0C．￢p：?x∈R，2x2+1＜0D．￢p：?x∈R，2x2+1＜0

分析 根据全称命题的否定是特称命题，即可得到结论．

解答 解：命题为全称命题，则命题的否定为：：?x∈R，2x2+1≤0，
故选：B

点评 本题主要考查含有量词的命题的否定，比较基础．

练习册系列答案
相关题目
20．sin（θ+75°）+cos（θ+45°）-$\sqrt{3}$cos（θ+15°）=（　　）
A．±1B．1C．-1D．0
1．设函数fn（x）=（1+x）n．
（1）若f2013（x）=a0+a1x+…+a2013x2013，
①求值：a0+a1+…+a2013
②求值：a1+a3+…+a2011+a2013
（2）当|x|≤1时，证明：fn（x）+fn（-x）≤2n（n∈N*）
18．已知$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$是一个平面内的三个向量，其中$\overrightarrow a$=（1，3）．
（1）若|$\overrightarrow c$|=2$\sqrt{10}$，$\overrightarrow c$∥$\overrightarrow a$，求$\overrightarrow c$及$\overrightarrow a•\overrightarrow c$；
（2）若|$\overrightarrow b$|=$\frac{{\sqrt{10}}}{2}$，且$\overrightarrow a$-3$\overrightarrow b$与2$\overrightarrow a$+$\overrightarrow b$垂直，求$\overrightarrow a$与$\overrightarrow b$的夹角．
5．曲线y=x2-2x与直线x=-1，x=l以及x轴所围图形的面积为2..
15．某学校有学生2500人，教师350人，后勤职工150人，为了调查对食堂服务的满意度，用分层抽样从中抽取300人，则学生甲被抽到的概率为（　　）
A．$\frac{1}{10}$B．$\frac{1}{300}$C．$\frac{1}{2500}$D．$\frac{1}{3000}$
2．定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1，p2，…，pn的“均倒数”．若已知正数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$，又bn=$\frac{{a}_{n}+1}{4}$，则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$的值为（　　）
A．$\frac{1}{2014}$B．$\frac{1}{2015}$C．$\frac{2013}{2014}$D．$\frac{2014}{2015}$
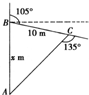19．如图，在某灾区的搜救现场，一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象，然后向右转105°，行进10m到达C处发现另一个生命迹象，这是它向右转135°可回到出发点，那么x=$\frac{10\sqrt{6}}{3}$（单位：m）．
20．已知函数f（x）=$\left\{\begin{array}{l}{xlnx，x＞a}\\{-{x}^{2}+2x+b，x≤a}\end{array}\right.$其中a≥0，b∈R．
（1）当a=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当a=1，b=1时，若函数y=f（x）-c有两个零点，求实数c的取值范围；
（3）当b=-2，若对任意的x1、x2∈R，都有f（x1）＜f（x2），求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网