题目内容
5.曲线y=x2-2x与直线x=-1,x=l以及x轴所围图形的面积为2..分析 先根据题意画出区域,然后依据图形利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答 解:根据题意画出图形,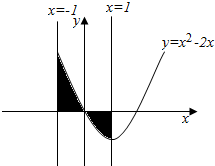
曲线y=x2-2x,与直线x=-1,x=1,以及x轴所围成的曲边梯形的面积为
${∫}_{-1}^{0}({x}^{2}-2x)dx+{∫}_{0}^{1}(2x-{x}^{2})dx$=($\frac{1}{3}{x}^{3}-{x}^{2}$)|${\;}_{-1}^{0}$+(x2-$\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=$\frac{4}{3}+\frac{2}{3}$=2;
故答案为:2
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于中档题

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.△ABC的外接圆半径为1,圆心为O,且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow 0$,则$\overrightarrow{OA}•\overrightarrow{BC}$的值为( )
| A. | -$\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{6}{5}$ | D. | $\frac{3}{5}$ |
10.已知命题p:?x∈R,2x2+1>0,则( )
| A. | ¬p:?x∈R,2x2+1≤0 | B. | ¬p:?x∈R,2x2+1≤0 | C. | ¬p:?x∈R,2x2+1<0 | D. | ¬p:?x∈R,2x2+1<0 |
17.设函数f(x)的导函数为f′(x),若对任意x∈R,都有f′(x)>f(x)成立,则( )
| A. | f(ln2015)<2015f(0) | |
| B. | f(ln2015)=2015f(0) | |
| C. | f(ln2015)>2015f(0) | |
| D. | f(ln2015)与2015f(0)的大小关系不确定 |
14.将函数y=$\frac{\sqrt{2}}{2}$(sinx+cosx)的图象上各点的横坐标伸长到原来的2倍,再向左平移$\frac{π}{2}$个单位,所得函数图象的解析式是( )
| A. | y=cos$\frac{x}{2}$ | B. | y=sin($\frac{x}{2}+\frac{3π}{4}$) | C. | y=-sin(2x+$\frac{π}{4}$) | D. | y=sin(2x+$\frac{3π}{4}$) |
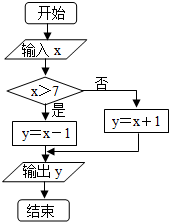 x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.