题目内容
7.某中学对高二甲、乙两个同类班级,进行“加强‘语文阅读理解’训练,对提高‘数学应用题’得分率的作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:| 60分以下 | 61-70分 | 71-80分 | 81-90分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | |
| 12乙班(人数) | 7 | 13 | 10 | 10 | 10 |
(I)试分析估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2x2列联表,根据以上数据,能杏有95%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助?
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
| P(x2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.028 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)根据所给的表格,看出两个班的所有的人数和两个班优秀的人数,分别用两个班优秀的人数除以总人数,得到两个班的优秀率.
(Ⅱ)根据所给的数据列出列联表,做出观测值,把观测值同临界值进行比较,得到有95%的把握认为有帮助.
解答 解:(Ⅰ)由题意知,甲、乙两班均有学生50人,
甲班优秀人数为30人,优秀率为$\frac{30}{50}$=60%,
乙班优秀人数为20人,优秀率为$\frac{20}{50}$=40%,
所以甲、乙两班的优秀率分别为60%和50%.…(4分)
(Ⅱ)
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | 30 | 20 | 50 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 50 | 50 | 100 |
因为x2=$\frac{100(30×30-20×20)^{2}}{50×50×50×50}$=4>3.841…(10分)
所以由参考数据知,有95%的把握认为有帮助. …(12分)
点评 本题考查列联表,考查独立性检验的作用,在解题时注意求这组数据的观测值时,注意数字的运算,因为这种问题一般给出公式,我们要代入公式进行运算,得到结果.

练习册系列答案
相关题目
18.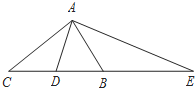 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |
2.设随机变量x~N(1,δ2),若P(x>2)=0.3,则P(x>0)等于( )
| A. | 0.3 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
16. 把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )
把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )
 把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )
把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )| A. | 第63行第2列 | B. | 第62行第12列 | C. | 第64行第30列 | D. | 第64行第60列 |
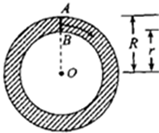 如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.
如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.