题目内容
已知函数
(Ⅰ)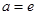 时,求
时,求 在
在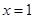 处的切线方程;
处的切线方程;
(Ⅱ)若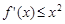 对任意的
对任意的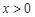 恒成立,求实数
恒成立,求实数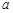 的取值范围;
的取值范围;
(Ⅲ)当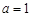 时,设函数
时,设函数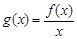 ,若
,若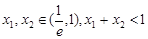 ,求证:
,求证: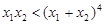 .
.
(Ⅰ)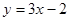 ;(Ⅱ)
;(Ⅱ)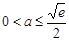 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)将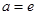 代入,求导即得;(Ⅱ)
代入,求导即得;(Ⅱ)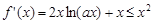 ,即
,即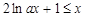 在
在 上恒成立. 不等式恒成立的问题,一般有以下两种考虑,一是分离参数,二是直接求最值.在本题中,设
上恒成立. 不等式恒成立的问题,一般有以下两种考虑,一是分离参数,二是直接求最值.在本题中,设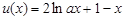 ,则
,则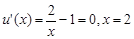 ,这里面不含参数
,这里面不含参数 了,求
了,求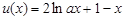 的最大值比较容易了,所可直接求最大值.(Ⅲ)本题首先要考虑的是,所要证的不等式与函数
的最大值比较容易了,所可直接求最大值.(Ⅲ)本题首先要考虑的是,所要证的不等式与函数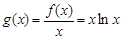 有什么关系?待证不等式可作如下变形:
有什么关系?待证不等式可作如下变形: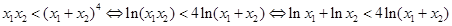 ,最后这个不等式与
,最后这个不等式与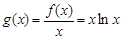 有联系吗?我们再往下看.
有联系吗?我们再往下看.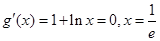 ,所以在
,所以在 上
上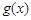 是增函数.
是增函数.
因为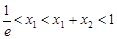 ,所以
,所以
即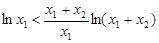 从这儿可以看出,有点联系了.
从这儿可以看出,有点联系了.
同理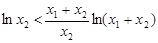 ,
,
所以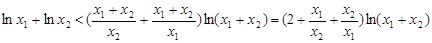 ,
,
与待证不等式比较,只要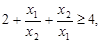 问题就解决了,而这由重要不等式可证,从而问题得证.
问题就解决了,而这由重要不等式可证,从而问题得证.
试题解析:(Ⅰ)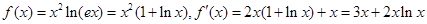 ,
,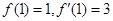 ,所以切线为:
,所以切线为: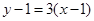 即
即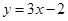 . 3分
. 3分
(Ⅱ) ,
,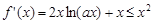 ,即
,即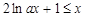 在
在 上恒成立
上恒成立
设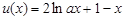 ,
,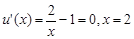 ,
,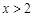 时,单调减,
时,单调减,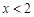 单调增,
单调增,
所以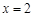 时,
时,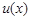 有最大值.
有最大值.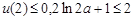 ,
,
所以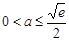 . 8分
. 8分
法二、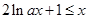 可化为
可化为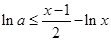 .
.
令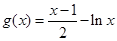 ,则
,则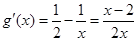 ,所以
,所以
所以 .
.
(Ⅲ)当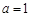 时,
时,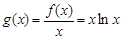 ,
,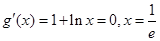 ,所以在
,所以在 上
上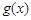 是增函数,
是增函数,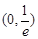 上是减函数.
上是减函数.
因为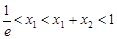 ,所以
,所以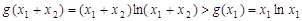
即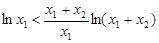 ,同理
,同理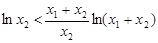 .
.
所以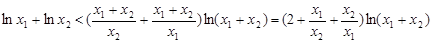
又因为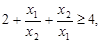 当且仅当“
当且仅当“ ”时,取等号.
”时,取等号.
又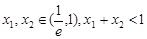 ,
,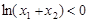 ,
,
所以 ,所以
,所以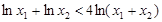 ,
,
所以: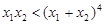 . 14分
. 14分
考点:1、导数的应用;2、不等式的证明.

练习册系列答案
相关题目
 ,
, (其中
(其中 为常数);
为常数); 和
和 有相同的极值点,求
有相同的极值点,求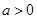 ,问是否存在
,问是否存在 ,使得
,使得 ,若存在,请求出实数
,若存在,请求出实数 ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数 ,设
,设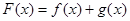
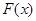 的单调区间
的单调区间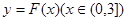 图象上任意一点
图象上任意一点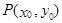 为切点的切线的斜率
为切点的切线的斜率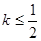 恒成立,求实数
恒成立,求实数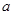 的最小值
的最小值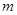 ,使得函数
,使得函数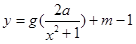 的图象与函数
的图象与函数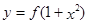 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数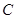 :
: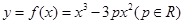 .
.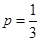 时,求曲线
时,求曲线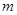 的两条直线与曲线
的两条直线与曲线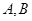 两点,求证:
两点,求证: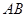 中点
中点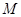 在曲线
在曲线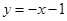 ,求
,求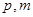 的值.
的值. .
. 垂直,求
垂直,求 的值;
的值; .
.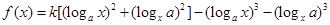 ,
,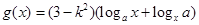 ,(其中
,(其中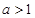 ),设
),设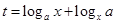 .
.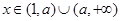 时,试将
时,试将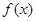 表示成
表示成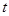 的函数
的函数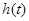 ,并探究函数
,并探究函数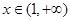 时,若存在
时,若存在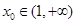 ,使
,使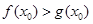 成立,试求
成立,试求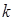 的范围.
的范围. .
.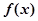 在区间
在区间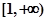 单调递增,求
单调递增,求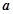 的最小值;
的最小值;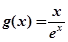 ,对
,对 ,使
,使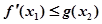 成立,求
成立,求 的范围.
的范围. 的前
的前 项和为
项和为 ,已知
,已知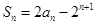 (n∈N*).
(n∈N*).
 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
.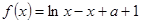
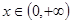 使得
使得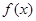 ≥0成立,求
≥0成立,求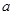 的范围
的范围  >1时,在(1)的条件下,
>1时,在(1)的条件下,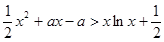 成立
成立