题目内容
已知函数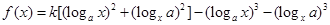 ,
,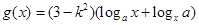 ,(其中
,(其中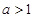 ),设
),设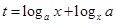 .
.
(Ⅰ)当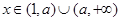 时,试将
时,试将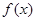 表示成
表示成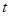 的函数
的函数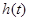 ,并探究函数
,并探究函数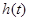 是否有极值;
是否有极值;
(Ⅱ)当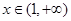 时,若存在
时,若存在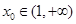 ,使
,使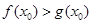 成立,试求
成立,试求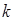 的范围.
的范围.
(Ⅰ)当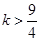 时
时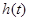 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当 时
时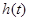 在定义域内无极值;
在定义域内无极值;
(Ⅱ)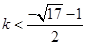 或
或
解析试题分析:(Ⅰ)观察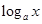 与
与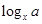 的特点
的特点 ,可得
,可得 ,
,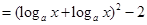 ,
, ,即可得到函数
,即可得到函数 ,观察此函数特征可想到对其求导得
,观察此函数特征可想到对其求导得 ,由二次函数的图象不难得出
,由二次函数的图象不难得出 在
在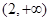 上有解的条件
上有解的条件 ,进而求出
,进而求出 的范围; (Ⅱ)由
的范围; (Ⅱ)由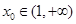 可得
可得 ,又由
,又由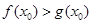 可得
可得 ,故可令函数
,故可令函数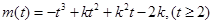 的最大值为正,对函数求导令其为0得
的最大值为正,对函数求导令其为0得 求出
求出 ,由
,由 与
与 ,和
,和 与
与 的大小关系对
的大小关系对 进行分类讨论,并求出各自情况的最大值,由最大值大于零即可求出
进行分类讨论,并求出各自情况的最大值,由最大值大于零即可求出 的范围.
的范围.
试题解析:(Ⅰ)∵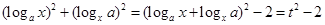 ,
, ,
,
∴ ∴
∴ (3分)
(3分)
设 是
是 的两根,则
的两根,则 ,∴
,∴ 在定义域内至多有一解,
在定义域内至多有一解,
欲使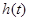 在定义域内有极值,只需
在定义域内有极值,只需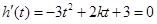 在
在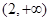 内有解,且
内有解,且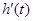 的值在根的左右两侧异号,∴
的值在根的左右两侧异号,∴ 得
得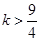 (6分)
(6分)
综上:当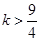 时
时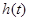 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当 时
时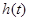 在定义域内无极值.
在定义域内无极值.
(Ⅱ)∵存在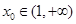 ,使
,使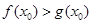 成立等价于
成立等价于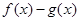 的最大值大于0,
的最大值大于0,
∵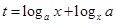 ,∴
,∴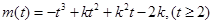 ,
,
∴ 得
得 .
.
当 时,
时,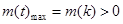 得
得 ;
;
当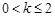 时,
时,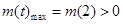 得
得 (12分)
(12分)
当 时,
时, 不成立 (13分)
不成立 (13分)
当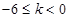 时,
时,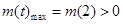 得
得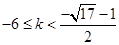 ;
;
当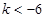 时,
时,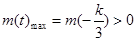 得
得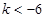 ;
;
综上得: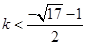 或
或 (16分)
(16分)
考点:1.代数式的化简;2.函数的极值;3.导数在函数中的运用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.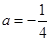 时,求函数
时,求函数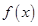 的单调区间;
的单调区间; 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围;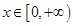 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数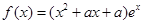 (
(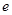 为自然对数的底数)。
为自然对数的底数)。 ,求函数
,求函数 的单调区间;
的单调区间;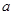 ,使函数
,使函数 上是单调增函数?若存在,求出
上是单调增函数?若存在,求出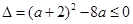
 ,又
,又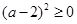 ,
,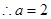
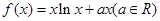 .
.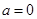 ,求
,求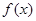 的最小值;
的最小值;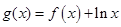 在区间
在区间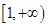 上为增函数,求实数
上为增函数,求实数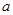 的取值范围;
的取值范围;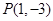 恰好能作函数
恰好能作函数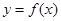 图象的两条切线,并且两切线的倾斜角互补,求实数
图象的两条切线,并且两切线的倾斜角互补,求实数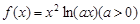
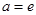 时,求
时,求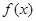 在
在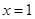 处的切线方程;
处的切线方程;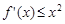 对任意的
对任意的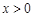 恒成立,求实数
恒成立,求实数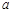 的取值范围;
的取值范围;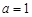 时,设函数
时,设函数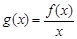 ,若
,若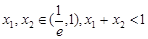 ,求证:
,求证: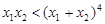 .
.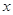 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量 (单位:件)
(单位:件) 的表达式;
的表达式; (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: )
)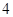 元,并且每件商品需向总店交
元,并且每件商品需向总店交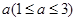 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为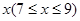 元时,一年的销售量为
元时,一年的销售量为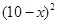 万件.
万件.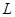 (万元)与每件商品的售价
(万元)与每件商品的售价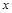 的函数关系式
的函数关系式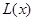 ;
; 的图象在与
的图象在与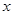 轴交点处的切线方程是
轴交点处的切线方程是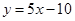 .
.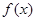 的解析式;
的解析式;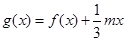 ,若
,若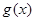 的极值存在,求实数
的极值存在,求实数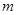 的取值范围以及函数
的取值范围以及函数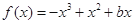 ,
,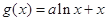 (
(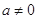 )
)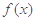 存在极值点,求实数b的取值范围;
存在极值点,求实数b的取值范围;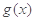 的单调区间;
的单调区间;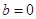 且
且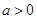 时,令
时,令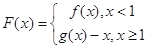 ,
,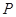 (
(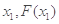 ),
),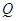 (
(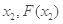 )为曲线y=
)为曲线y=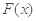 上的两动点,O为坐标原点,能否使得
上的两动点,O为坐标原点,能否使得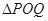 是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由
是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由