题目内容
已知函数 .
.
(1)若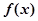 在区间
在区间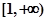 单调递增,求
单调递增,求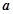 的最小值;
的最小值;
(2)若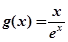 ,对
,对 ,使
,使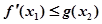 成立,求
成立,求 的范围.
的范围.
(1)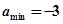 ;(2)
;(2)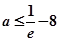 .
.
解析试题分析:(1)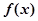 在区间
在区间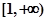 单调递增,则
单调递增,则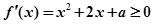 在
在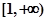 恒成立.
恒成立.
分离变量得: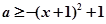 ,所以a大于等于
,所以a大于等于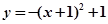 的最大值即可.
的最大值即可.
(2)对 ,使
,使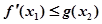 ,则应有
,则应有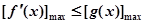
下面就分别求出 ,
,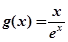 的最大值,然后解不等式
的最大值,然后解不等式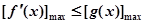 即得a的范围.
即得a的范围.
试题解析:(1)由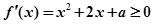 在
在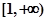 恒成立
恒成立
得: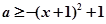 而
而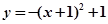 在
在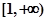 单调递减,从而
单调递减,从而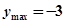 ,
,
∴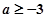
∴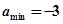 6分
6分
(2)对 ,使
,使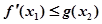 ∴
∴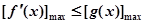
 在
在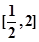 单调递增
单调递增
∴ 8分
8分
又 ∴
∴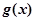 在
在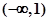 单调递增,在
单调递增,在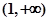 单调递减
单调递减
∴在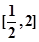 上,
上,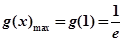 ∴
∴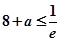
则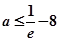 12分
12分
考点:导数的应用.

练习册系列答案
相关题目
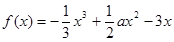 ,
,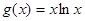
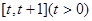 上的最小值;
上的最小值;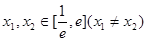 ,使方程
,使方程
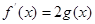 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)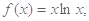
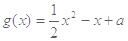 .
.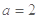 时,求
时,求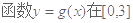 上的值域;
上的值域;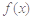 在
在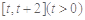 上的最小值;
上的最小值;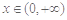 ,都有
,都有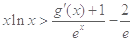 成立
成立
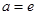 时,求
时,求 在
在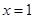 处的切线方程;
处的切线方程;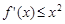 对任意的
对任意的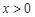 恒成立,求实数
恒成立,求实数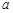 的取值范围;
的取值范围;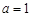 时,设函数
时,设函数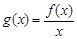 ,若
,若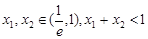 ,求证:
,求证: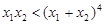 .
.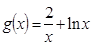 ,
,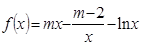 ,
,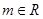 .
.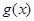 的极值点;
的极值点;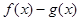 在
在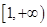 上为单调函数,求
上为单调函数,求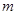 的取值范围;
的取值范围;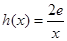 ,若在
,若在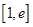 上至少存在一个
上至少存在一个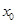 ,使得
,使得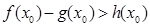 成立,求
成立,求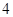 元,并且每件商品需向总店交
元,并且每件商品需向总店交 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为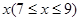 元时,一年的销售量为
元时,一年的销售量为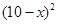 万件.
万件.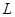 (万元)与每件商品的售价
(万元)与每件商品的售价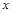 的函数关系式
的函数关系式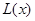 ;
; .
.
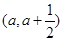 其中
其中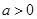 上存在极值,求实数
上存在极值,求实数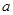 的取值范围;
的取值范围;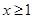 时,不等式
时,不等式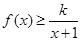 恒成立,求实数
恒成立,求实数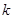 的取值范围.
的取值范围.