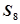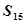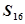题目内容
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出严格的证明.
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出严格的证明.
(1) a1=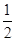 . a2=
. a2=
(2)猜想Sn=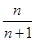 ,n=1,2,3,….
,n=1,2,3,….
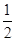 . a2=
. a2=
(2)猜想Sn=
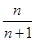 ,n=1,2,3,….
,n=1,2,3,….(1)先令n=1,则s1-1即a1-1是方程的一个根,因而建立关于a1的方程求出a1的值.同理再利用n=2时,求出a2.
(2)由条件可知(Sn-1)2-an(Sn-1)-an=0,化简得S-2Sn+1-anSn=0,
然后利用n≥2时,an=Sn-Sn-1,把an代入上式,消去an,就找到了sn与sn-1之间的递推关系,求出s1,s2,s3,然后观察规律,归纳出sn,再利用数学归纳法证明即可
(1)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,于是(a1-1)2-a1(a1-1)-a1=0,解得a1=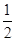 . 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-
. 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-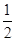 , 于是(a2-
, 于是(a2-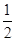 )2-a2(a2-
)2-a2(a2-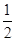 )-a2=0,解得a2=
)-a2=0,解得a2=
(2)由题设(Sn-1)2-an(Sn-1)-an=0,S-2Sn+1-anSn=0.当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①由(1)得S1=a1=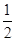 ,S2=a1+a2=
,S2=a1+a2=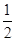 +
+ =
=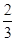 .
.
由①可得S3=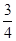 .由此猜想Sn=
.由此猜想Sn=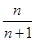 ,n=1,2,3,….
,n=1,2,3,….
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=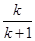 ,当n=k+1时,由①得Sk+1=
,当n=k+1时,由①得Sk+1=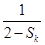 ,即Sk+1=
,即Sk+1=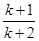 ,故n=k+1时结论也成立.
,故n=k+1时结论也成立.
综上,由(i)、(ii)可知Sn=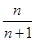 对所有正整数n都成立.
对所有正整数n都成立.
(2)由条件可知(Sn-1)2-an(Sn-1)-an=0,化简得S-2Sn+1-anSn=0,
然后利用n≥2时,an=Sn-Sn-1,把an代入上式,消去an,就找到了sn与sn-1之间的递推关系,求出s1,s2,s3,然后观察规律,归纳出sn,再利用数学归纳法证明即可
(1)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,于是(a1-1)2-a1(a1-1)-a1=0,解得a1=
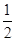 . 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-
. 当n=2时,x2-a2x-a2=0有一根为S2-1=a2-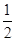 , 于是(a2-
, 于是(a2-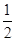 )2-a2(a2-
)2-a2(a2-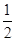 )-a2=0,解得a2=
)-a2=0,解得a2=
(2)由题设(Sn-1)2-an(Sn-1)-an=0,S-2Sn+1-anSn=0.当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①由(1)得S1=a1=
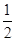 ,S2=a1+a2=
,S2=a1+a2=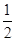 +
+ =
=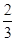 .
.由①可得S3=
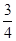 .由此猜想Sn=
.由此猜想Sn=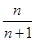 ,n=1,2,3,….
,n=1,2,3,….下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=
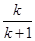 ,当n=k+1时,由①得Sk+1=
,当n=k+1时,由①得Sk+1=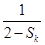 ,即Sk+1=
,即Sk+1=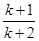 ,故n=k+1时结论也成立.
,故n=k+1时结论也成立. 综上,由(i)、(ii)可知Sn=
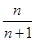 对所有正整数n都成立.
对所有正整数n都成立.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的通项是关于x的不等式
的通项是关于x的不等式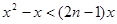
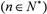 的解集中整数的个数.
的解集中整数的个数.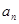 并且证明
并且证明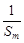 +
+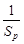 ≥
≥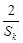 ;
;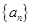 满足
满足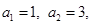
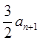 是
是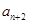 与
与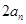 的等差中项
的等差中项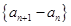 是等比数列;
是等比数列;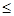 xn<xn+1<3;
xn<xn+1<3;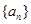 中,
中,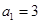 ,前
,前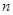 项和为
项和为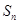 ,等比数列
,等比数列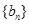 各项均为正数,
各项均为正数,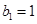 ,且
,且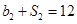 ,
,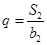
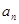 与
与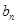 ;
;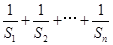
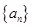 是等差数列,
是等差数列,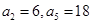 ;数列
;数列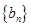 的前n项和是
的前n项和是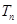 ,且
,且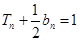 .
.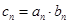 ,求
,求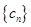 的前n项和
的前n项和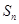
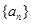 (公差不为零)和等差数列
(公差不为零)和等差数列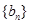 ,如果关于
,如果关于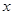 的方程
的方程 有解,那么以下九个方程已知等差数列
有解,那么以下九个方程已知等差数列 ,
, 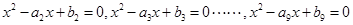 中,
中,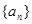 中,
中,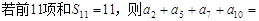 ( )
( )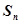 是等差数列
是等差数列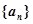 的前
的前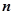 项和,若
项和,若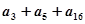 是一个确定的常数,则在数列
是一个确定的常数,则在数列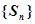 中也是确定常数的项是 ( )
中也是确定常数的项是 ( )