题目内容
函数f(x)=x2-2x-3,定义数列{xn}如下:x1=2,xn+1是过两点P(4,5)、Qn(xn,f(xn))的直线PQn与x轴交点的横坐标。
(Ⅰ)证明:2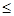 xn<xn+1<3;
xn<xn+1<3;
(Ⅱ)求数列{xn}的通项公式。
(Ⅰ)证明:2
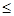 xn<xn+1<3;
xn<xn+1<3;(Ⅱ)求数列{xn}的通项公式。
见解析
解:(1)用数学归纳法证明
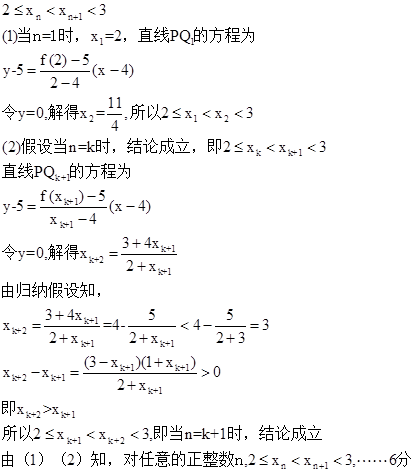
(2)

【命题意图】本试题主要考查了数列的通项公式以及函数与数列的相结合的综合运用。先从函数入手,表示直线方程,从而得到交点坐标,再结合数列的知识解决。
【点评】以函数为背景,引出点的坐标,并通过直线与坐标轴的交点的得到数列的通项公式。
既考查了直线方程,又考查了函数解析式,以及不等式的证明,试题比较综合,有一定的难度。做这类试题那就是根据已知条件,一步一步的翻译为代数式,化简得到要找的关系式即可。

练习册系列答案
相关题目
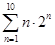 = .
= .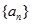 的首项
的首项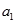 及公差
及公差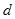 都是整数,前
都是整数,前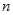 项和为
项和为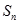 ,若
,若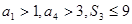 ,设
,设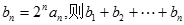 的结果为 .
的结果为 .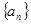 的前
的前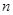 项和为
项和为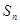 ,且
,且 .
.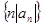 的前
的前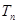 ,求数列
,求数列 的通项公式.
的通项公式.
 个等式为 .
个等式为 .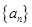 中,
中, ,
,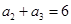 ,则
,则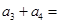
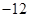
 中,若
中,若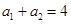 ,
, 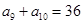 ,则
,则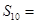
 中,前
中,前 项和
项和 ,则
,则 ▲ .
▲ .