题目内容
数列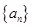 是等差数列,
是等差数列,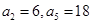 ;数列
;数列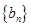 的前n项和是
的前n项和是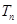 ,且
,且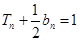 .
.
(1) 求数列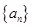 的通项公式; (2) 求证:数列
的通项公式; (2) 求证:数列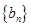 是等比数列;
是等比数列;
(3) 记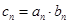 ,求
,求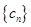 的前n项和
的前n项和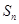
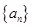 是等差数列,
是等差数列,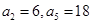 ;数列
;数列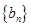 的前n项和是
的前n项和是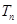 ,且
,且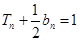 .
.(1) 求数列
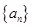 的通项公式; (2) 求证:数列
的通项公式; (2) 求证:数列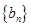 是等比数列;
是等比数列;(3) 记
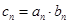 ,求
,求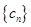 的前n项和
的前n项和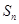
(Ⅰ) 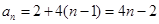 .(Ⅱ)见解析;(Ⅲ)
.(Ⅱ)见解析;(Ⅲ)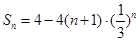 .
.
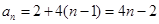 .(Ⅱ)见解析;(Ⅲ)
.(Ⅱ)见解析;(Ⅲ)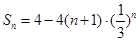 .
. 据等差数列通项公式∵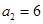 ,
,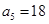 ,∴
,∴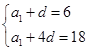 ,得出首项,公差;进而求得通项;
,得出首项,公差;进而求得通项;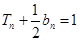 是和与通项的关系,根据当
是和与通项的关系,根据当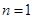 时,
时,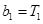 ,当
,当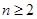 时,
时,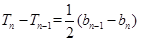 ,即
,即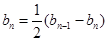 ,证明
,证明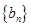 是等比数列;
是等比数列;
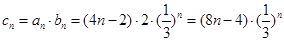 是差比数列,求和用错位相减法,注意项数的对齐。
是差比数列,求和用错位相减法,注意项数的对齐。
解:(Ⅰ)设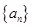 的公差为
的公差为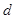 ,则:
,则: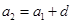 ,
,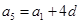 ,
,
∵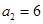 ,
,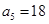 ,∴
,∴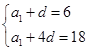 ,∴
,∴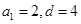 .
.
∴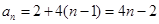 . …………………………………………5分
. …………………………………………5分
(Ⅱ)当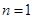 时,
时,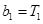 ,由
,由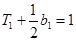 ,得
,得 .
.
当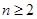 时,
时,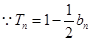 ,
,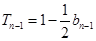 ,
,
∴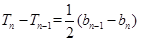 ,即
,即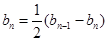 .
.
∴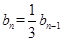 .
.
∴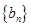 是以
是以 为首项,
为首项,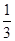 为公比的等比数列. …………………………………5分
为公比的等比数列. …………………………………5分
(Ⅲ)由(2)可知: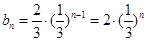 .
.
∴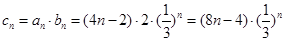 .
.
∴ .
.
∴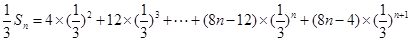 .
.
∴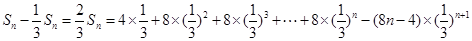
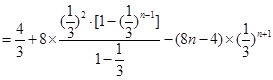
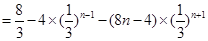 .
.
∴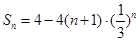 . …………………………………………………6分
. …………………………………………………6分
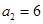 ,
,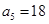 ,∴
,∴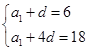 ,得出首项,公差;进而求得通项;
,得出首项,公差;进而求得通项;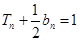 是和与通项的关系,根据当
是和与通项的关系,根据当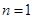 时,
时,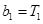 ,当
,当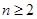 时,
时,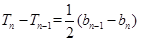 ,即
,即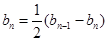 ,证明
,证明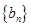 是等比数列;
是等比数列;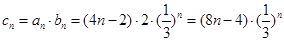 是差比数列,求和用错位相减法,注意项数的对齐。
是差比数列,求和用错位相减法,注意项数的对齐。解:(Ⅰ)设
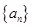 的公差为
的公差为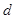 ,则:
,则: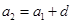 ,
,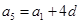 ,
,∵
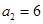 ,
,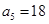 ,∴
,∴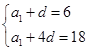 ,∴
,∴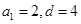 .
. ∴
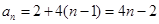 . …………………………………………5分
. …………………………………………5分(Ⅱ)当
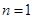 时,
时,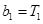 ,由
,由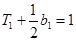 ,得
,得 .
. 当
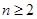 时,
时,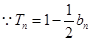 ,
,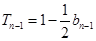 ,
,∴
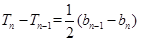 ,即
,即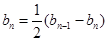 .
. ∴
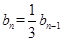 .
. ∴
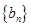 是以
是以 为首项,
为首项,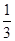 为公比的等比数列. …………………………………5分
为公比的等比数列. …………………………………5分(Ⅲ)由(2)可知:
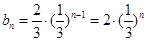 .
. ∴
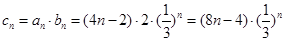 .
. ∴
 .
.∴
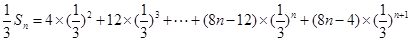 .
.∴
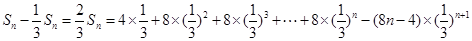
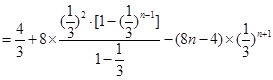
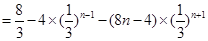 .
. ∴
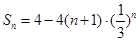 . …………………………………………………6分
. …………………………………………………6分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
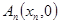 满足:
满足: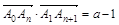 ,其中
,其中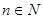 ,又已知
,又已知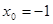 ,
,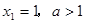 .
.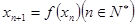 ,求
,求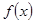 的表达式;
的表达式;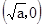 ,记
,记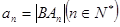 ,且
,且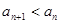 成立,试求a的取值范围;
成立,试求a的取值范围;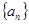 的前n项和为
的前n项和为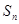 ,试求:
,试求: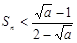 。
。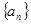 的前
的前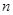 项和为
项和为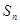 ,且
,且 .
.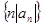 的前
的前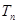 ,求数列
,求数列 的通项公式.
的通项公式.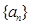 前
前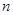 项和为
项和为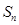 , 满足
, 满足 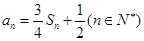 .
.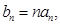 求数列
求数列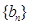 的前
的前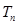 ;
;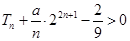 对任意的
对任意的 恒成立,求实数
恒成立,求实数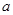 的取值范围.
的取值范围.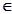 N*,均有S n>0
N*,均有S n>0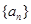 中,若
中,若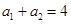 ,
, 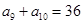 ,则
,则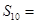
 中,
中, ,前
,前 项和为
项和为 ,则
,则 = .
= .