题目内容
9.已知复数$z=a(1+i)+\frac{2}{i}$(a∈R,i为虚数单位)为实数,则${∫}_{0}^{a}$($\sqrt{4-{x}^{2}}$+x)dx的值为( )| A. | 2+π | B. | 2+$\frac{π}{2}$ | C. | 4+2π | D. | 4+4π |
分析 由复数定义易得a=2,由定积分的几何意和定积分的计算可得.
解答 解:∵$z=a(1+i)+\frac{2}{i}$=a+(a-2)i,(a∈R,i为虚数单位)为实数,∴a=2,
∴${∫}_{0}^{a}$($\sqrt{4-{x}^{2}}$+x)dx=${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx+${∫}_{0}^{2}$xdx,
由定积分的几何意义可知${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx表示圆x2+y2=4面积的四分之一,为π,
∴=${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx+${∫}_{0}^{2}$xdx=π+$\frac{1}{2}{x}^{2}$|${\;}_{0}^{2}$=π+2,
故选:A.
点评 本题考查复数的基本概念和定积分的求解,属基础题

练习册系列答案
相关题目
20.曲线y=ax2-ax+1(a≠0)在点(0,1)处的切线与直线2x+y+1=0垂直,则a=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
17. 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的表面积是( )| A. | 92 | B. | $16\sqrt{2}+80$ | C. | 80 | D. | $16\sqrt{2}+92$ |
14.若点P的坐标为(x0,y0),曲线C的方程为F(x,y)=0,则“F(x0,y0)=0”是“点P在曲线C上”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
1.若圆x2+y2-6x+6y+14=0关于直线l:ax+4y-6=0对称,则直线l的斜率是( )
| A. | 6 | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
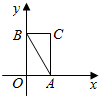 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)