题目内容
15.已知向量$\overrightarrow{b}$为单位向量,向量$\overrightarrow{a}$与向量$\overrightarrow{b}$夹角为60°,则对任意的正实数t,|t$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
分析 由题意利用两个向量的数量积的定义,结合二次函数的性质求得它的最小值.
解答 解:由题意可得$\overrightarrow{a}$$•\overrightarrow{b}$=|$\overrightarrow{a}$|×1×cos60°=$\frac{|\overrightarrow{a}|}{2}$,对任意的正实数t,
∵|t$\overrightarrow{a}$-$\overrightarrow{b}$|2=(t$\overrightarrow{a}$)2-2t$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=(t$\overrightarrow{a}$)2-t|$\overrightarrow{a}$|+1=(t|$\overrightarrow{a}$|-$\frac{1}{2}$)2+$\frac{3}{4}$,
∴当t|$\overrightarrow{a}$|=$\frac{1}{2}$时,|t$\overrightarrow{a}$-$\overrightarrow{b}$|2有最小值$\frac{3}{4}$,
即|t$\overrightarrow{a}$-$\overrightarrow{b}$|最小值为$\sqrt{\frac{3}{4}}$=$\frac{\sqrt{3}}{2}$,
故选:C
点评 本题主要考查两个向量的数量积的定义,求向量的模,二次函数的性质,属于中档题

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
20.曲线y=ax2-ax+1(a≠0)在点(0,1)处的切线与直线2x+y+1=0垂直,则a=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
4.现有20个数,它们构成一个以1为首项,-2为公比的等比数列,若从这20个数中随机抽取一个数,则它大于8的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
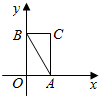 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)