题目内容
14.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,则(a-c)2+(b-d)2的最小值为( )| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
分析 由题设条件:b+2a2-6lna=0,设b=y,a=x,则有:y=6lnx-2x2;2c-d+6=0,设c=x,d=y,则有:y=2x+6,所以(a-c)2+(b-d)2就是曲线y=6lnx-2x2与直线y=2x+6之间的最小距离的平方值,由此能求出(a-c)2+(b-d)2的最小值
解答 解:∵实数a、b、c、d满足:
(b+2a2-6lna)2+|2c-d+6|=0
∴b+2a2-6lna=0,设b=y,a=x,
则有:y=6lnx-2x2
2c-d+6=0,设c=x,d=y,则有:y=2x+6,
∴(a-c)2+(b-d)2就是曲线y=6lnx-2x2与直线y=2x+6之间的最小距离的平方值,
对曲线y=6lnx-2x2求导:
y′(x)=$\frac{6}{x}$-4x,
与y=2x+6平行的切线斜率k=2=$\frac{6}{x}$-4x,
解得:x=1或x=-$\frac{3}{2}$(舍去)
把x=1代入y=6lnx-2x2,得:y=-2,
即切点为(1,-2)
切点到直线y=2x+6的距离:
d=$\frac{10}{\sqrt{5}}$=2$\sqrt{5}$
即d2=20,(a-c)2+(b-d)2的最小值就是20.
故选:C.
点评 本题考查导数在求解函数最值中的应用,对数运算法则的应用,是中档题,解题时要注意点到直线的距离公式的合理运用以及转化思想的应用.

练习册系列答案
相关题目
5.阅读如图所示的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为( )
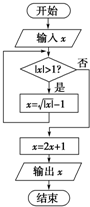

| A. | 9 | B. | 3 | C. | 1 | D. | -1 |
9.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,(a-c)2+(b-d)2的最小值为m,则函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({0,\frac{1}{4}})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
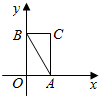 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)