题目内容
16.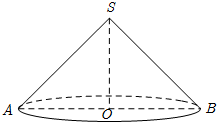 如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.
如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.
分析 设圆锥的底面半径为r,则圆锥的高也为r.结合圆锥体积为$\frac{8}{3}$π,可得r的值,代入圆锥的表面积公式,可得答案.
解答 解:设圆锥的底面半径为r,则圆锥的高也为r.
由$\frac{1}{3}π{r^2}•r=\frac{8}{3}π$,得:r=2,
故母线长$l=2\sqrt{2}$.…(2分)
圆锥的底面积${S_底}=π{r^2}=4π$,…(3分)
圆锥的侧面积${S_侧}=πrl=4\sqrt{2}π$,…(5分)
故圆锥的表面积${S_全}=(4+4\sqrt{2})π$.…(6分)
点评 本题考查的知识点是旋转体,圆锥的体积和表面积公式,难度不大,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
1.若圆x2+y2-6x+6y+14=0关于直线l:ax+4y-6=0对称,则直线l的斜率是( )
| A. | 6 | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
5.阅读如图所示的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为( )
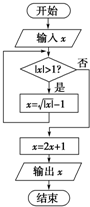

| A. | 9 | B. | 3 | C. | 1 | D. | -1 |
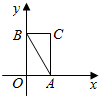 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)